چند جفت خرگوش توسط یک جفت در یک سال ایجاد می شود؟

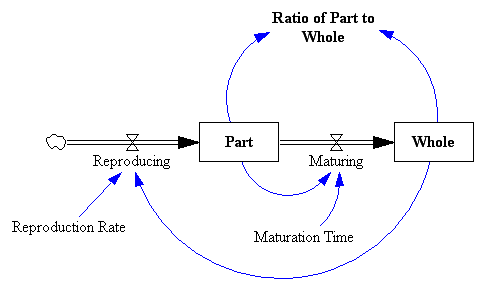
اعداد فیبوناچی اغلب به صورت هندسی، با مارپیچ یا کاشی کاری مربع نشان داده می شوند، اما ناتیلوس منشأ آنها نیست. اخیراً فهمیدم که این دنباله برای اولین بار به عنوان راه حلی برای آزمایش فکری مدلسازی پویا گزارش شد که توسط لئوناردو پیزانو (فیبوناچی) در شاهکار سال 1202 خود، Liber Abaci ارائه شد.

چند جفت خرگوش توسط یک جفت در یک سال ایجاد می شود؟

مردی یک جفت خرگوش با هم در یک مکان محصور داشت و می‌خواهد بداند در یک سال چند خرگوش از آن جفت خلق شده است در حالی که طبیعتاً در یک ماه یک جفت دیگر را می‌آورند و در دومی ماه متولدین برای تحمل نیز. از آنجا که جفت نوشته شده در بالا در ماه اول سوراخ شد، آن را دو برابر خواهید کرد. دو جفت در یک ماه وجود خواهد داشت. یکی از اینها، یعنی اولی، در ماه دوم خرس می کند، و بنابراین در ماه دوم 3 جفت وجود دارد. از این تعداد در یک ماه دو باردار می شوند و در ماه سوم 2 جفت خرگوش به دنیا می آیند و به این ترتیب در ماه 5 جفت وجود دارد. در این ماه 3 جفت حامله می شوند و در ماه چهارم 8 جفت که 5 جفت آن 5 جفت دیگر را می آورند. اینها به 8 جفت اضافه می شوند و در ماه پنجم 13 جفت می شوند. این 5 جفتی که در این ماه به دنیا می آیند در این ماه جفت نمی شوند، اما 8 جفت دیگر حامله هستند و به این ترتیب در ماه ششم 21 جفت وجود دارد. [ص284] به اینها 13 جفتی که در ماه هفتم متولد شده اند اضافه می شود. در این ماه 34 جفت وجود خواهد داشت. به این 21 جفت که در ماه هشتم متولد شده اند اضافه می شود. در این ماه 55 جفت وجود خواهد داشت. به اینها 34 جفتی که در ماه نهم متولد شده اند اضافه می شود. 89 جفت در این ماه وجود خواهد داشت. به اینها 55 جفتی که در ماه دهم متولد شده اند دوباره اضافه می شوند. در این ماه 144 جفت وجود خواهد داشت. به این 89 جفتی که در ماه یازدهم متولد شده اند دوباره اضافه می شود. در این ماه 233 جفت وجود خواهد داشت.

منبع: http://www.math.utah.edu/~beebe/software/java/fibonacci/liber-abaci.html

راه حل دنباله معروف فیبوناچی است که می توان آن را به صورت یک سری تکراری نوشت.

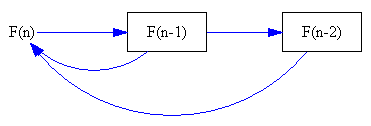
F(n) = F(n-1)+F(n-2), F(0)=F(1)=1

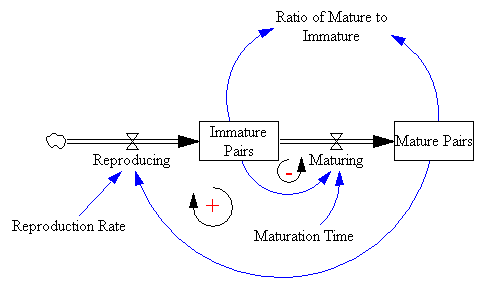
با این حال، این نمایش کمی بیش از حد انتزاعی است که بلافاصله ارتباط با خرگوش ها را آشکار می کند. در عوض، من ترجیح می‌دهم برای ساختن یک نمایش عملیاتی، به شرح مشکل فیبوناچی برگردم:

جفت‌های خرگوش بالغ در یک انبار نگهداری می‌شوند («فضای محصور معین» فیبوناچی)، و هر ماه یک جفت جدید تولید می‌کنند (یعنی نرخ تولید مثل = 1/ماه). مدل‌سازی جفت‌های نر و ماده به جای خرگوش‌های منفرد، نگرانی در مورد ترکیب جنسیت را کنار می‌زند. نکته مهم این است که یک ماه تاخیر بین تولد و تولید مثل وجود دارد (“در ماه دوم کسانی که برای باردار شدن نیز متولد شده اند”). این تاخیر توسط سهام جفت نابالغ گرفته می شود. خرگوش ها در این آزمایش فکری برای همیشه زندگی می کنند، بنابراین هیچ خروجی از جفت های بالغ وجود ندارد.

اگر بازنمایی زمان گسسته مدل را بنویسید، و واحدها را نادیده بگیرید و فرض کنید که TIME STEP = نرخ تولید مثل = زمان بلوغ = 1، می توانید رابطه بین سری و ساختار سهام-جریان را ببینید:

Mature Pairs(t) = Mature Pairs(t-1) + Maturing

Immature Pairs(t) = Immature Pairs(t-1) + Reproducing - Maturing

جایگزینی بالغ = جفت نابالغ و تولید مثل = جفت بالغ،

Mature Pairs(t) = Mature Pairs(t-1) + Immature Pairs(t-1)

Immature Pairs(t) = Immature Pairs(t-1) + Mature Pairs(t-1) - Immature Pairs(t-1) = Mature Pairs(t-1)

پس:

Mature Pairs(t) = Mature Pairs(t-1) + Mature Pairs(t-2)

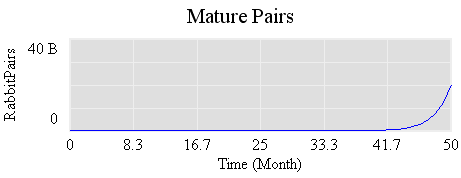
مدل حاصل دارای دو حلقه بازخورد است: یک حلقه منفی جزئی که بر بلوغ جفت‌های نابالغ حاکم است و یک حلقه مثبت خرگوش در حال تولید مثل. جمعیت خرگوش به دلیل حلقه مثبت تمایل به انفجار دارد:

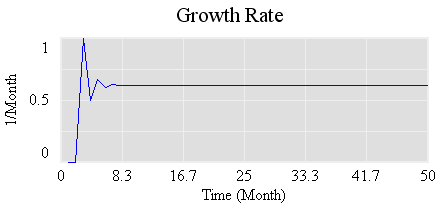
در عرض چهار سال، تقریباً به اندازه انسان روی زمین خرگوش وجود دارد، بنابراین “فضای محصور معین” بهتر است بزرگ باشد. پس از یک دوره گذرا اولیه، سرعت رشد به سرعت کاهش می یابد:

مقدار حالت پایدار آن 0.61803… (61.8٪ در ماه) است که مزدوج نسبت طلایی است. اگر نام متغیرها را تغییر دهید، می توانید رابطه با تفسیر کاشی کاری و نسبت طلایی را ببینید:

مانند هر چیزی که به صورت تصاعدی رشد می کند، اعداد فیبوناچی به سرعت بزرگ می شوند. صدم 354,224,848,179,261,915,075 است.

مانند قبل، می‌توانیم ترفند بردار ویژه را برای سرکوب حالت رشد بازی کنیم. سیستم توسط ماتریس توضیح داده شده است:

-1 1
 1 0

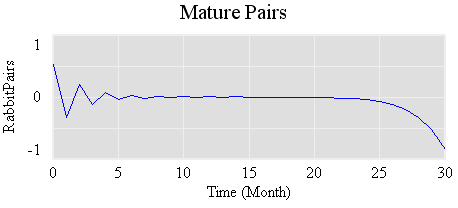
که دارای مقادیر ویژه {-1.618033988749895، 0.6180339887498949} است – به ظاهر نسبت طلایی توجه کنید. اگر مدل را با بردار ویژه مقدار ویژه منفی، {-0.8506508083520399, 0.5257311121191336} مقداردهی اولیه کنیم، می‌توانیم جمعیت خرگوش را تحت کنترل درآوریم، حداقل تا زمانی که نویز عددی حالت رشد را تحریک کند، نزدیک به زمان 25:

مشکل این است که ما برای انجام این کار به خرگوش های منفی نیاز داریم، خرگوش های نابالغ -.850653، بنابراین این یک راه حل فیزیکی قابل تحقق نیست (که احتمالا تضمین می کند که به زودی در قانون معرفی خواهد شد).

من این موضوع را با بچه‌هایم مطرح کردم، و آنها بلافاصله به سراغ فیزیک این مشکل رفتند: «خرگوش‌ها برای همیشه زنده نیستند. اندازه قفس شما چقدر است؟ غذای خرگوش داری؟ تن غذای خرگوش؟ اگر همه نرها یا ترکیبات متفاوتی از نر و ماده داشته باشید، چه؟

تعمیم ساختار برای تولید توالی های دیگر آسان است. به عنوان مثال، با فرض اینکه خرگوش های بالغ فقط دو ماه زندگی می کنند، توالی پادووان به دست می آید. معادل آن نسبت طلایی 1.3247 است، یعنی جمعیت خرگوش کندتر رشد می کند و در حدود 32٪ در ماه رشد می کند، همانطور که انتظار دارید از آنجایی که عمر خرگوش ها کوتاه تر است.

مدل در کتابخانه است.