مقاله نقاط اوج
بحث جالبی در مورد نقاط اوج (tipping points) جنگل در مقاله جدیدی در Science وجود دارد:
انعطافپذیری جهانی جنگلهای استوایی و ساوانا به انتقال بحرانی
Global Resilience of Tropical Forest and Savanna to Critical Transitions
مارینا هیروتا، میلنا هولمگرن، اگبرت اچ وان نس، مارتن شفر
پیشنهاد شده است که جنگلهای استوایی و ساوانا میتوانند حالتهای پایدار جایگزین را نشان دهند، که دلالت بر انتقالهای بحرانی در نقاط اوج در پاسخ به آب و هوای تغییریافته یا سایر محرکها دارد. تاکنون، شواهدی برای این ایده مبهم باقی مانده است، و مدل های آب و هوایی یکپارچه پاسخ های پوشش گیاهی صاف را فرض می کنند. ما دادههای مربوط به توزیع پوشش درختان را در آفریقا، استرالیا و آمریکای جنوبی تجزیه و تحلیل کردیم تا شواهد قوی برای وجود سه جاذبه متمایز نشان دهیم: جنگل، ساوانا و یک ایالت بدون درخت. بازسازی تجربی حوضه های جاذبه نشان می دهد که انعطاف پذیری ایالت ها به شیوه ای جهانی با بارش متفاوت است. این نتایج امکان شناسایی مناطقی را فراهم می کند که جنگل یا ساوانا به آسانی ممکن است به یک حالت جایگزین تبدیل شود و راه را برای نسل جدیدی از مدل های آب و هوایی همراه هموار می کند.
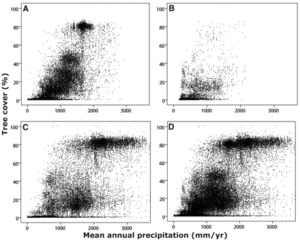
مقاله ارزش خواندن دارد. این یک مدل شبیه سازی صریح ارائه نمی دهد، اما مفهوم را به خوبی توصیف می کند. مشاهدات اساسی این است که در توزیع پوشش جنگلی در مقابل بارش، خوشه بندی وجود دارد:
Hirota et al., Science 14 October 2011
در ذهنیت رگرسیون معمولی، مشاهده می کنید که برخی از مکان ها با بارندگی 2 متری ساوانا هستند و برخی دیگر جنگل هستند و به دنبال متغیرهای توضیحی دیگری (خاک، عرض جغرافیایی، …) می روید که تفاوت را توضیح می دهند. ممکن است چیزی یاد بگیرید، یا اگر پوشش جنگل نه تنها در ورودی های مختلف غیرخطی باشد، بلکه وابسته به حالت باشد، ممکن است دچار مشکل شوید. نویسندگان فکر دوم را دنبال می کنند: ممکن است چندین حالت پایدار برای پوشش جنگلی در سطح معینی از بارش وجود داشته باشد.
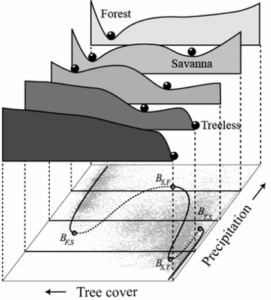
آنها از توزیع پوشش جنگلی بارش و مشاهده استفاده می کنند که در یک سیستم مرتبه اول در معرض نویز، توزیع پوشش جنگلی مشاهده شده چیزی در مورد تابع پتانسیل پوشش جنگل نشان می دهد. آنها با استفاده از هموارسازی هسته، تابع های پتانسیل جنگل را برای سطوح مختلف بارش بازسازی می کنند:
Hirota et al., Science 14 October 2011
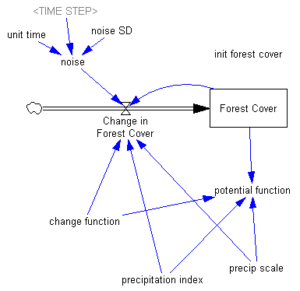
من فکر کردم که بازی با آن سرگرم کننده به نظر می رسد، بنابراین یک مدل کوچک ساختم که به طور کیفی پویایی را به تصویر می کشد:
بخش دشوار بازسازی تابع پتانسیل بدون داده بود. معلوم شد که نوشتن معادله سرعت برای تغییر پوشش جنگل در بارش متوسط (“تابع تغییر” در مدل) آسان تر است، و سپس زمانی که بارندگی زیاد یا کم است، آن را با یک عبارت اضافی شیب دار (کج شدن) کنید. سپس تابع پتانسیل از رابطه آن با مشتق بازسازی می شود، dz/dt = f(z) = -dV/dz، که z پوشش جنگل و V پتانسیل است.
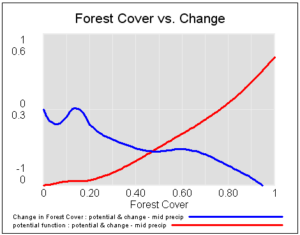
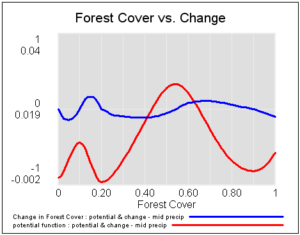
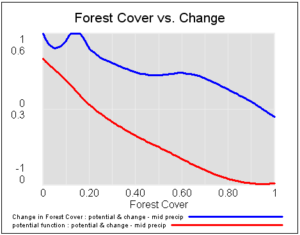
آن، پتانسیل ها و میدان های برداری (نرخ تغییر) زیر را در بارندگی کم، متوسط و زیاد به نتیجه می دهد:
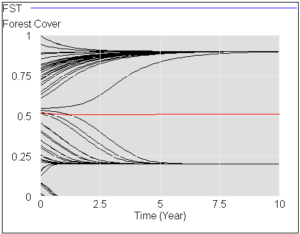
اگر این سیستم را در سطوح مختلف پوشش جنگلی راه اندازی کنید، برای بارش متوسط، می توانید سه جاذبه پایدار در درختان صفر، ساوانا (20 درصد پوشش درخت) و جنگل (90 درصد پوشش درخت) را ببینید.
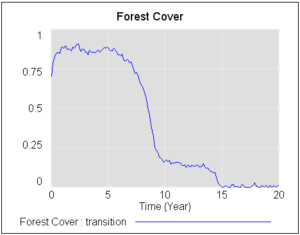
اگر با یک جنگل پایدار و کمی سر و صدا شروع کنید، سپس به تدریج بارش را کاهش دهید، می بینید که پاسخ جنگل صاف نیست.
جنگل تا حدود سال 8 پایدار است، سپس به طور ناگهانی به ساوانا منتقل می شود. سرانجام در حدود سال 14، ساوانا ناپدید می شود و حالتی بی درخت جایگزین آن می شود. جنگل تا زمانی که شاخص بارش به حدود 0.3 برسد، به ساوانا منتقل نمی شود، حتی اگر ساوانا در بین دو ایالت بسیار زودتر، با بارش حدود 0.55 پایدارتر می شود. و در حالی که حالت ساوانا در بارندگی کم کاملاً ناپایدار نمی شود، نویز سیستم را از آستانه به حالت بدون درخت با پتانسیل پایین تر می برد.
نتیجه خالص این است که فکر کردن به چنین سیستمی از منظری ایستا و خطی شما را به دردسر میاندازد. و اگر در اطراف چنین سیستمی زندگی میکنید، با توجه به تغییر آب و هوا، این انتقال میتواند ناگهانی و غافلگیرکننده باشد (آتش سوزی ممکن است یکی از مکانیسمهای انحرافی باشد).
مدل در کتابخانه من است.