مشکلات تطبیق الگو فقط برای مقایسههای شهودی رفتار سهام و جریانهای مرتبط اعمال نمیشود. آنها همچنین در مورد آمار اعمال می شوند. این بدان معنی است که برای مثال، یک رگرسیون خطی مانند
stock = a + b*flow + c*time + error
به احتمال زیاد به اشتباه جدی می رود. با این حال، این مانع از ورود چنین چیزهایی به ادبیات بررسی شده نمی شود. یک خطای شبه آماری رایجتر این است که دو چیز را که ممکن است مرتبط باشند، اندازهگیری کنید، روند خطی آنها را اندازهگیری کنید و اگر روندها مطابقت نداشتند، رابطه را جعلی اعلام کنید. این استدلال ساختگی همچنان یکی از سرگرمیهای رایج برای شکاکان آب و هوا است، که میپرسند چگونه دما در دورهای که انتشار گازهای گلخانهای افزایش مییابد پایین میآید؟ (این مثال را ببینید.) این نوع استدلال آماری ساده لوحانه، با مدل های ذهنی ایستا از پدیده های پویا، به سختی به شکاکان آب و هوا محدود می شود.
با توجه به پویایی، در واقع بسیار آسان است که ببینیم چگونه چنین چیزهایی می توانند رخ دهند. در اینجا یک مثال کاملتر از یک موقعیت واقعی آورده شده است:
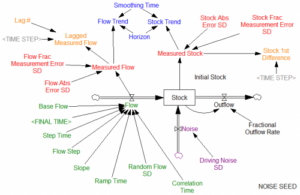
در هسته، جریان یکسانی را داریم که انباشت را هدایت می کند. جریان توسط انواع ورودی های آزمایشی تعیین می شود، بنابراین ما هنوز نگران علیت دایره ای بین سهام و جریان نیستیم. به طور بالقوه بازخوردی از انباشت برای خروج وجود دارد، اگرچه این به طور پیش فرض فعال نیست. انباشت همچنین تحت تأثیرات تصادفی دیگری قرار دارد، با انحراف استاندارد که توسط Driving Noise SD ارائه شده است. ما لزوماً نمی توانیم انباشت و جریان را مستقیماً مشاهده کنیم. مشاهدات ما در معرض خطای اندازه گیری هستند. برای اهدافی که بهطور لحظهای آشکار میشوند، ممکن است برخی دستکاریهای ساده در اندازهگیریهای خود مانند تاخیر و تفاوت انجام دهیم. ما همچنین می توانیم روند انباشت و جریان را اندازه گیری کنیم. توجه داشته باشید که این هنوز هم کمی واقعیت را ساده میکند، زیرا اندازهگیری جریان بهجای نیاز به فرآیند ادغام خود آنگونه که فیزیک میخواهد، آنی است. هیچ عارضه ای مانند داده های از دست رفته یا فواصل اندازه گیری نابرابر وجود ندارد.
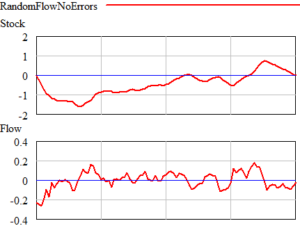
حالا برای یک آزمایش ابتدا فرض کنید که جریان تصادفی است (نویز صورتی) و هیچ خطای اندازه گیری، صدای رانندگی یا خروجی وجود ندارد. در آن صورت، این را می بینید:
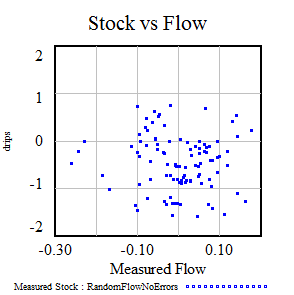
وان در واقع میتواند با تقسیم کردن آنها به قسمتهای ظاهری، نتایج خرافی در مورد سریهای زمانی انباشت و جریان در بالا بگیرد، اما این احتمالاً گمراهکننده است، مگر اینکه به صراحت به وان حمام فکر کنید. با نگاهی به نمودار پراکندگی جریان-انباشت، به نظر می رسد که هیچ رابطه ای وجود ندارد:
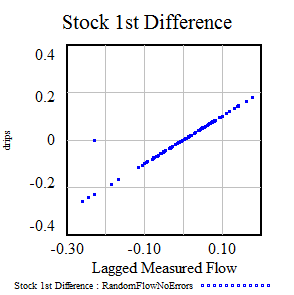
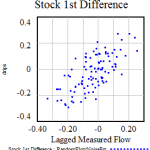
البته، ما می دانیم که این اشتباه است، زیرا ما مدل را با علیت Flow->Stock کامل ساختیم. ترفند آماری معمول برای آشکار کردن رابطه، خنثی کردن ادغام با گرفتن اولین تفاوت دادههای موجودی است. وقتی این کار را انجام میدهید، نمودار تغییر انباشت در مقابل جریان (یک دوره تاخیر برای محاسبه تفاوت)، رابطه دوباره ظاهر میشود:
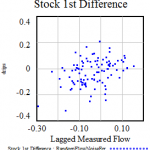
متأسفانه، این یک روش بسیار قوی نیست. مشتقات نویز را تقویت میکنند، و اشتباه کردن چیزهای دیگر آسان است، مانند ناهماهنگی تاخیرهای گزارش. با اضافه کردن نویز رانندگی و خطاهای اندازه گیری به آخرین آزمایش، می توانیم ببینیم که چگونه شیب مشاهده شده رابطه در مه ناپدید می شود:
قرعهکشیهای تصادفی خوش شانس در مقابل بدشانس، با روابطی که تا حدی تا کاملاً توسط نویز پنهان شده است.
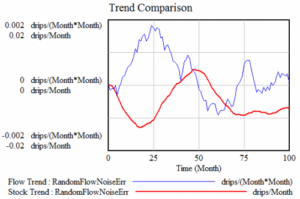
در هر صورت، مقایسه روند جریان و انباشت آموزنده نیست. در واقع، مقایسه روند مشتقات هر دو طرف معادله را می گیرد، بنابراین ادغام را خنثی نمی کند – فقط آن را به سطح دیگری منتقل می کند و نویز را تقویت می کند. در اینجا مقایسه ای از تخمین روند (از مرتبه دوم صاف) از آزمایش پر سر و صدا بالا آمده است:
در واقع مهم نیست که از چه الگوریتم هموارسازی یا رگرسیونی برای تخمین روندها استفاده می کنید، زیرا هیچ مقداری از دستکاری نمی تواند این واقعیت را جبران کند که دینامیک وان حمام را نادیده می گیرید.
در مواردی که نویز تفاوت را از بین میبرد، هنوز هم میتوان با پیچیدهتر شدن (تخمین یک مدل پویا، با فیلتر کالمن)، اطلاعاتی را از آزمایشهای بالا بهدست آورد، اما برای این کار باید کاملاً در وان حمام غوطهور شوید.
به روز رسانی: مدل در کتابخانه من است.