زمان گسسته بوی بدی می‌دهد

مدل‌سازی زمان گسسته اغلب راحت، گاهی اوقات درست و اغلب خطرناک است.

اغلب مدل‌هایی را می‌بینید که در زمان گسسته بیان می‌شوند، مانند:

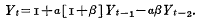
Y(t) = C(t) + I(t)
C(t) = aY(t-1)
I(t) = b(C(t) - C(t-1))

این مدل ضریب-شتاب دهنده ساموئلسون است. همین نماد در آمار، اقتصاد، ABM و بسیاری از زمینه‌های دیگر رایج است.

خب، مشکل چیست؟

بیشتر دنیای واقعی در زمان گسسته اتفاق نمی‌افتد. چند تصمیم، مانند حراج‌های برق، در فواصل منظم رخ می‌دهند، اما اینها استثنا هستند. بیشتر اوقات ما در مقیاس‌های زمانی طولانی نسبت به پدیده‌های اساسی مدل‌سازی می‌کنیم و عوامل یا ذرات یا هر چیز ناهمگن زیادی با تأخیرها و فواصل تصمیم‌گیری متنوع داریم.
زمان گسسته می‌تواند به طور مصنوعی ناپایدار باشد. یک سیستم پیوسته پایدار را می‌توان با شبیه‌سازی در یک بازه گسسته بسیار بزرگ ناپایدار کرد. یک سیستم گسسته ممکن است نوسان کند، در حالی که معادل پیوسته آن نوسان نمی‌کند.
نمی‌توانید به راحتی تأثیر گام زمانی را بر پایداری آزمایش کنید. س: اگر مدل زمان گسسته شما با یک ردیف اکسل در هر بازه اجرا می‌شود، چگونه یک بازه 1/2 یا 1/12 برابر بزرگتر را برای مقایسه آزمایش می‌کنید؟ ج: نمی‌توانید. حتی اگر به ذهن شما برسد که امتحان کنید، دردسر زیادی خواهد داشت.
بازه اندازه‌گیری لزوماً مقیاس زمانی پویای مربوطه نیست. اغلب گام زمانی یک مدل گسسته از بازه اندازه‌گیری در داده‌ها ناشی می‌شود. هیچ چیز جادویی در مورد آن بازه، با توجه به نحوه عملکرد واقعی سیستم، وجود ندارد.
مفاهیم انبارها و جریان‌ها و حالت سیستم مبهم هستند. (نمودار مدل ساموئلسون در بالا را ببینید.) عدم سازگاری انبار جریان می‌تواند منجر به مشکلات دیگری مانند عدم حفظ مقادیر فیزیکی شود.
واحدها مبهم هستند. این نتیجه شماره 5 است. وقتی حالات و نرخ‌های تغییر آنها به طور مساوی در یک معادله ظاهر می‌شوند، تعیین اینکه چه چیزی چیست دشوار است. مدل‌های گسسته تمایل دارند با ثابت‌های زمانی ضمنی و سایر پارامترهای پنهان پر شوند.
بیشتر تأخیرها گسسته نیستند. در مدل ساموئلسون، خروجی به خروجی سال گذشته بستگی دارد. اما چرا نه هفته گذشته یا قرن گذشته؟ و چرا یک تأخیر باید دقیقاً از 3 دوره تشکیل شود، نه اینکه در طول زمان توزیع شود؟ (این انتقاد به برخی از معادلات دیفرانسیل تأخیری نیز اعمال می‌شود.)
بیشتر منطق گسسته نیست. وقتی زمان با خوشحالی در گام‌های قفل گسسته پیش می‌رود، به راحتی می‌توان در تفکر گسسته گرفتار شد: “اگر قیمت ذرت کمتر از قیمت ذرت سال گذشته است، خوک بخرید.” این ممکن است مدل خوبی برای یک کشاورز باشد، اما فاقد ظرافت است و مطمئناً مجموع کشاورزان متنوع را نشان نمی‌دهد. این تقصیر زمان گسسته به خودی خود نیست، اما این دو اغلب دست در دست هم دارند. (این یکی از بسیاری از نقص‌های مدل معروف لوینتال و مارچ است.)

مطمئناً مواردی وجود دارد که نیاز به شبیه‌سازی زمان گسسته دارند (در اینجا یک فصل خوب در مورد تجزیه و تحلیل چنین سیستم‌هایی وجود دارد). اما بیشتر اوقات، یک رویکرد پیوسته نقطه شروع بهتری است، همانطور که جی فارستر 50 سال پیش نوشت. بهترین رویکرد گاهی اوقات ترکیبی است، با یک جریان زیرین زمان پیوسته برای “فیزیک” مدل، اما با فرآیندهای اندازه‌گیری که با نمونه‌گیری صریح در فواصل گسسته نشان داده می‌شوند.

بنابراین، اگر یک مدل زمان گسسته نامناسب را در کشوی جوراب تحلیلی خود پیدا کردید، چه؟ نترسید، می‌توانید آن را تبدیل کنید.

مدل adstock را در نظر بگیرید که نشان دهنده اثرات تجمعی تبلیغات است:

Ad Effect = f(Adstock)
Adstock(t) = Advertising(t) + k*Adstock(t-1)

توجه داشته باشید که k به طول عمر تبلیغات مربوط است، اما از آنجا که نسبت به بازه گسسته است، به طور گمراه کننده‌ای بدون بعد است. همچنین، بازه در 1 واحد زمانی ثابت است و بدون مقیاس‌بندی k قابل تغییر نیست.

همچنین توجه داشته باشید که اثر تبلیغات یک جزء آنی دارد. معمولاً بین قرار گرفتن در معرض تبلیغات و اقدام تأخیری وجود دارد. این تأخیر ممکن است در برخی موارد، مانند خریدهای درون برنامه‌ای، ناچیز باشد، اما معمولاً برای رفتار درون فروشگاهی ناچیز نیست.

می‌توانید این را با استفاده از یک تأخیر گسسته به زبان Vensim ترجمه کنید:

Adstock = Advertising + k*Previous Adstock ~ GRPs
Previous Adstock = DELAY FIXED( Adstock, Ad Life, 0 ) ~ GRPs
Ad life = ... ~ weeks

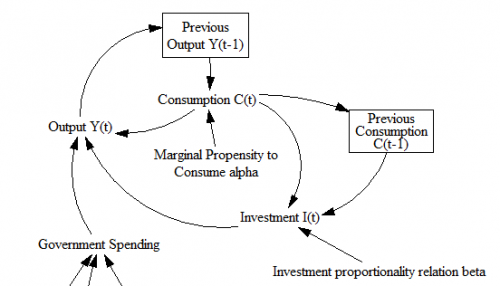
این کاربردی است، اما پیشرفت چندانی نیست. بسیار بهتر است تشخیص دهیم که Adstock (تعجب!) انباری است که در طول زمان تغییر می‌کند:

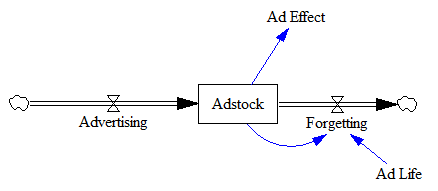
Ad Effect = f(Adstock) ~ dimensionless
Adstock = INTEG( Advertising - Forgetting, 0 ) ~ GRPs
Advertising = ... ~ GRPs/week
Forgetting = Adstock / Ad Life ~ GRPs/week
Ad Life = ... ~ weeks

اکنون طول عمر تبلیغات یک تفسیر دنیای واقعی با بعد دارد و می‌توانید با هر گام زمانی که نیاز دارید، مستقل از پارامترها (تا زمانی که به اندازه کافی کوچک باشد) شبیه‌سازی کنید.

یک مشکل جزئی وجود دارد: اثر تبلیغات آنی که در بالا ذکر کردم. این زمانی اتفاق می‌افتد که، برای مثال، بازه داده هفتگی است و تبلیغات منتشر شده در هفته انتشار خود تأثیر دارند – به عنوان مثال، آگهی فروش دوشنبه فروش آخر هفته را هدایت می‌کند.

دو راه حل برای این وجود دارد:

“تقلب” این است که از طریق یک پارامتر “اثر هفته جاری”، کمی از جریان فعلی تبلیغات را در adstock مؤثر قرار دهید. این کمی پیچیده است، زیرا شما را در گام زمانی هفتگی قفل می‌کند. می‌توانید با هزینه پیچیدگی بیشتر در معادلات، آن را تعمیم دهید.
یک راه حل اساسی‌تر این است که مدل را در یک گام زمانی ظریف‌تر از بازه داده اجرا کنید. این یک مدل تمیزتر به شما می‌دهد و شما چیزی را با توجه به کالیبراسیون از دست نمی‌دهید (حداقل در Vensim/Ventity).

گاهی اوقات، شما با بیش از یک حالت تأخیری در سمت راست معادله مواجه می‌شوید، مانند گنجاندن Y(t-1) و Y(t-2) در مدل ساموئلسون (بالا). این معمولاً نشان دهنده یک تأخیر با یک ساختار پیچیده (به عنوان مثال، مرتبه دوم یا بالاتر) یا برخی از اثرات مرتبه بالاتر دیگر است. به طور کلی، شما باید بتوانید به این حالات نام و تفسیر بدهید (مانند ساخت Y و C در مدل ساموئلسون). اگر نمی‌توانید، موهای خود را نکنید. ممکن است اصل آن بد فرمول بندی شده باشد. در عوض، با در نظر گرفتن انبارها و جریان‌ها، از ابتدا به موضوع فکر کنید.