تابع مرموز TREND – مدل ونسیم

این پست به معنای واقعی کلمه در حال ترند شدن است.

اکثر نرم‌افزارهای پویایی سیستم شامل یک جفت تابع TREND و FORECAST هستند. به دلایل تاریخی، اینها معمولاً ساده‌ترین ساختار مرتبه اول ممکن هستند، که برای مدل‌های پیوسته و قطعی خوب است، اما برای برنامه‌های کاربردی با نویز یا داده‌های واقعی بهترین نیست. این وضعیت با این واقعیت پیچیده‌تر می‌شود که اکسل یک تابع TREND دارد که واقعاً FORECASTing است، به علاوه توابع FORECAST جدیدتر با روش‌هایی که ممکن است با عملکرد معمول SD متفاوت باشند. پویایی کسب و کار یک تابع TREND مرتبه سوم را توصیف می‌کند که برای برنامه‌های کاربردی دنیای واقعی بسیار بهتر است.

در نتیجه این تنوع، فکر می‌کنم اندازه‌گیری و پیش‌بینی روند به طور غیرضروری مرموز باقی مانده است، بنابراین من مدل زیر را برای مقایسه چندین رویکرد ساختم.

هدف

هدف توابع TREND و FORECAST مدل‌سازی شکل‌گیری انتظارات به گونه‌ای است که با آنچه افراد در مدل واقعاً انجام می‌دهند، مطابقت داشته باشد.

این می‌تواند معانی بسیار متنوعی داشته باشد. در بسیاری از موارد، افراد تفکر رسمی را به مشاهده و پیش‌بینی پدیده مورد نظر اختصاص نمی‌دهند. در این صورت، انتظارات تطبیقی ممکن است مدل خوبی باشد. پیاده‌سازی در SD تابع SMOOTH است. استفاده از SMOOTH برای تنظیم انتظارات می‌گوید که افراد انتظار دارند آینده مانند گذشته باشد و تغییرات در شرایط را فقط به تدریج درک می‌کنند. این عالی است اگر متغیر پیش‌بینی شده در واقع ثابت باشد، یا حداقل اگر تغییرات در مقایسه با زمان ادراک کند باشد. از طرف دیگر، برای یک وضعیت سریع در حال تحول مانند COVID19، تأخیر می‌تواند کشنده باشد – به معنای واقعی کلمه.

برای هر چیزی که در واقع در حال تغییر است (یا افرادی که درک می‌کنند در حال تغییر است)، منطقی است که تغییرات را با نوعی مدل به آینده پیش‌بینی کنیم. برای بخش کوچکی از واقعیت، این ممکن است به معنای یک مدل پیچیده باشد: رگرسیون چندگانه، یادگیری ماشین یا نوعی مدل علی کالیبره شده، برای مثال. با این حال، اکثر چیزها مشمول این نوع بررسی پیچیده نیستند. در عوض، انتظارات احتمالاً با نوعی برون‌یابی ساده از روندهای گذشته به آینده شکل می‌گیرند.

در برخی موارد، چیزهایی که ظاهراً به روشی پیچیده مدل‌سازی می‌شوند، به دلیل طبیعت انسان، ممکن است شبیه برون‌یابی به نظر برسند. پیش‌بینی‌کنندگان انتظارات پیشینی از آنچه “پیش‌بینی‌های مدل خوب” به نظر می‌رسند، بر اساس انتظارات تطبیقی-برون‌یابی نسبتاً ساده و فرآیندهای اجتماعی، شکل می‌دهند و از آن انتظارات برای فیلتر کردن نتایجی که قابل قبول تلقی می‌شوند، استفاده می‌کنند. این باعث می‌شود نتایج پیچیده بسیار شبیه برون‌یابی به نظر برسند. با این حال، هر چه مدل بهتر باشد، انجام این کار دشوارتر است.

هدف، به هر حال، عموماً استفاده از توابع شبیه روند برای پیش‌بینی نیست. برون‌یابی ممکن است در برخی موارد کاملاً منطقی باشد، به ویژه در جایی که به نتیجه اهمیت زیادی نمی‌دهید. اما به طور کلی، شما با یک مدل پیچیده‌تر بهتر هستید – کل هدف SD و سایر روش‌ها پرداختن به بازخورد و غیرخطی‌هایی است که باعث می‌شود برون‌یابی و سایر روش‌های ساده‌لوحانه اشتباه پیش بروند. از طرف دیگر، برون‌یابی ساده ممکن است برای ایجاد یک پیش‌بینی ساده یا صفر عالی باشد تا به عنوان یک معیار برای مقایسه با رویکردهای بهتر استفاده شود.

مبانی

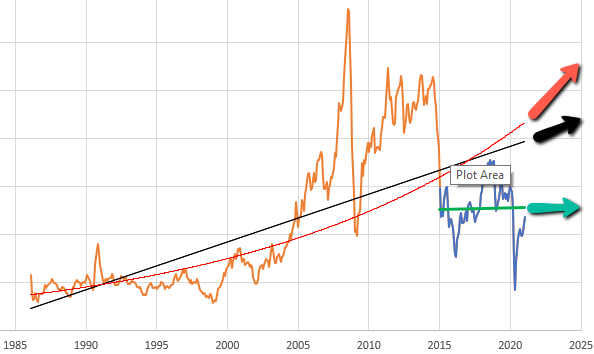
بنابراین، فرض کنیم می‌خواهید انتظارات را برای چیزی مدل‌سازی کنید که افراد آن را (به طور بالقوه) به طور پیوسته در حال افزایش یا کاهش می‌دانند. می‌توانید به St. Louis FRED مراجعه کنید و مجموعه‌های اقتصادی زیادی مانند این پیدا کنید – تولید ناخالص داخلی، قیمت‌ها و غیره. در اینجا قیمت نقدی نفت خام وست تگزاس اینترمدیت آمده است:

با توجه به این داده‌ها، بلافاصله انتخاب‌های زیادی وجود دارد. با فکر کردن به کسی که امروز سرمایه‌گذاری را مشروط به قیمت‌های نفت آینده انجام می‌دهد، آیا باید به صورت خطی (خطوط سیاه و سبز) یا نمایی (خط قرمز) برون‌یابی کنند؟ آیا باید از کل مجموعه (سیاه و قرمز) یا فقط چند سال آخر (سبز) استفاده کنند؟ هر یک از اینها پیش‌بینی متفاوتی برای آینده را نشان می‌دهد.

فرض کنیم ایده‌هایی در مورد افق پیش‌بینی، حساسیت مطلوب به نویز و غیره داریم. چگونه واقعاً یک روند را ایجاد می‌کنیم؟ یک گزینه رگرسیون خطی است، که فقط یک روش رسمی برای ترسیم یک خط مستقیم است که با برخی داده‌ها مطابقت دارد. به خوبی کار می‌کند، اما معایبی دارد. اول، به تمام داده‌ها در طول بازه وزن مساوی و به هر چیزی خارج از بازه وزن صفر اختصاص می‌دهد. این ممکن است مدل ضعیفی برای فرآیندهای ادراکی باشد، جایی که جدیدترین داده‌ها بیشترین برجستگی را برای تصمیم‌گیرنده دارند. دوم، از نظر محاسباتی و ذخیره‌سازی فشرده است: باید ریاضیات زیادی انجام دهید و هر نقطه داده را در پنجره مورد نظر پیگیری کنید. این خوب است اگر در یک صفحه گسترده قرار داشته باشد، اما اگر در ذهن کسی قرار داشته باشد، خوب نیست.

برازش خطی به زیرمجموعه‌ای از داده‌های قیمت نقدی WTI.

توابع شبیه روند یک ساده‌سازی ظریف ایجاد می‌کنند که معایب رگرسیون را برطرف می‌کند. این بر اساس مشاهده زیر است:*

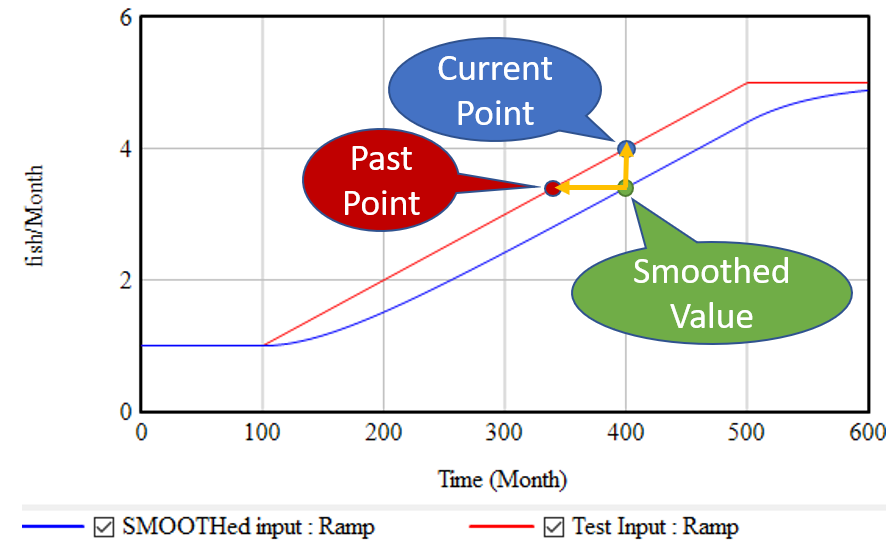
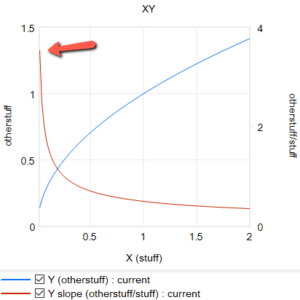
اگر، مانند بالا، یک ورودی در حال رشد (خط قرمز) را بگیرید و آن را به صورت نمایی هموار کنید (با استفاده از تابع SMOOTH یا یک ساختار هدف-شکاف مرتبه اول معادل)، خط آبی را دریافت می‌کنید: یک شیب دیگر، که ورودی را با تأخیری برابر با زمان هموارسازی عقب می‌اندازد. این بدان معناست که در ماه 400، دو نقطه را می‌دانیم: مقدار فعلی ورودی و مقدار فعلی ورودی هموار شده. اما مقدار هموار شده نشان دهنده مقدار گذشته ورودی است، در این مورد 60 ماه قبل. بنابراین، می‌توانیم از این دو نقطه برای تعیین شیب خط قرمز استفاده کنیم:

(1) slope = (current - smoothed) / smoothing time

این شیب از نظر واحدهای ورودی در هر زمان است. اغلب محاسبه شیب کسری به جای آن راحت است، که رشد را به عنوان افزایش کسری در ورودی در هر واحد زمان بیان می‌کند:

(2) fractional slope = (current - smoothed) / smoothed / smoothing time

این همان چیزی است که توابع ساده TREND در نرم‌افزار SD معمولاً گزارش می‌کنند. توجه داشته باشید که اگر مقدار هموار شده به 0 برسد، منفجر می‌شود، در حالی که روش خطی (1) این کار را نمی‌کند.

اگر فکر می‌کنیم رشد نمایی است، نه یک شیب خطی، می‌توانیم نرخ رشد را در زمان پیوسته محاسبه کنیم:

(3) fractional growth rate = LN( current / smoothed ) / smoothing time

این مزایا و معایبی دارد. بدیهی است، اگر یک کمیت واقعاً به صورت نمایی در حال رشد است، باید به این روش اندازه‌گیری شود. اما اگر در حال مدل‌سازی نحوه تفکر واقعی افراد هستیم، ممکن است زمانی که رفتار اساسی نمایی است، به صورت خطی برون‌یابی کنند، و در نتیجه رشد آینده را بسیار دست کم بگیرند. توجه داشته باشید که ایده پیش‌بینی به صورت نمایی فرض می‌کند که مقادیر درگیر مثبت هستند.

هنگامی که شیب خط (تخمین زده شده) را می‌دانید، می‌توانید آن را از طریق روشی که با اندازه‌گیری مطابقت دارد، به آینده برون‌یابی کنید:

(1b) future value = current + slope * forecast horizon
(2b) future value = current * (1 + fractional slope * forecast horizon)
(3b) future value = current * EXP( fractional growth rate * forecast horizon )

توابع معمول FORECAST از (2b) استفاده می‌کنند.

*بحث خوبی در مورد این موضوع در ضمیمه L پویایی صنعتی، در اطراف شکل L-3 وجود دارد.

 

اصلاحات

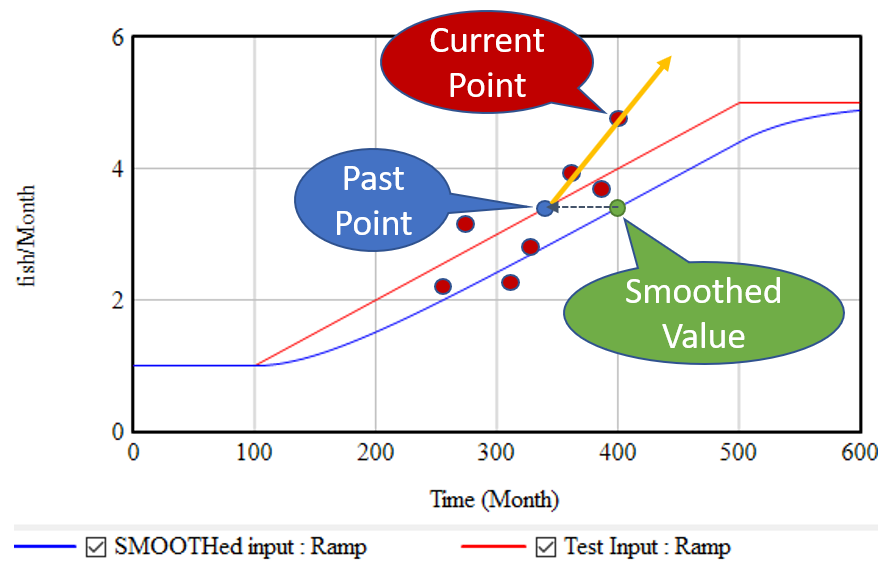
استراتژی بالا فضیلت سادگی بسیار زیاد را دارد: شما فقط باید یک انبار اضافی را پیگیری کنید و محاسبات مورد نیاز برای برون‌یابی حداقل است. برای مدل‌های پیوسته عالی کار می‌کند. متأسفانه، در برابر نویز و ناپیوستگی‌ها مقاومت چندانی ندارد. در نظر بگیرید که اگر ورودی یک خط صاف نباشد، بلکه مجموعه‌ای از نقاط پر سر و صدا پراکنده در اطراف خط باشد، چه اتفاقی می‌افتد:

تابع SMOOTH داده‌ها را فیلتر می‌کند، بنابراین نقطه گذشته (آبی) ممکن است هنوز به روند ورودی اساسی (خط قرمز) بسیار نزدیک باشد. با این حال، برون‌یابی (خط نارنجی) فقط به نقطه گذشته و نقطه جریان واحد متکی است. بنابراین هر نویز یا ناپیوستگی در نقطه جریان می‌تواند به طور چشمگیری بر تخمین شیب و پیش‌بینی‌های آینده تأثیر بگذارد. این خوب نیست.

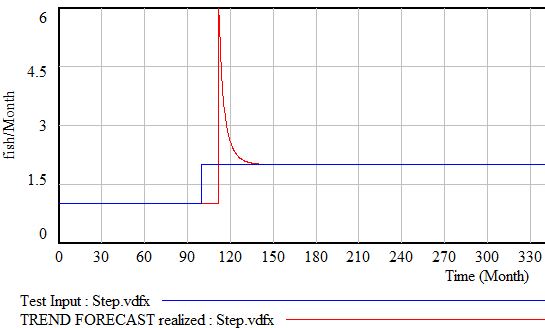
رفتارهای منحرف مشابهی در صورت ورودی تابع پالس یا پله رخ می‌دهد. برای مثال:

 

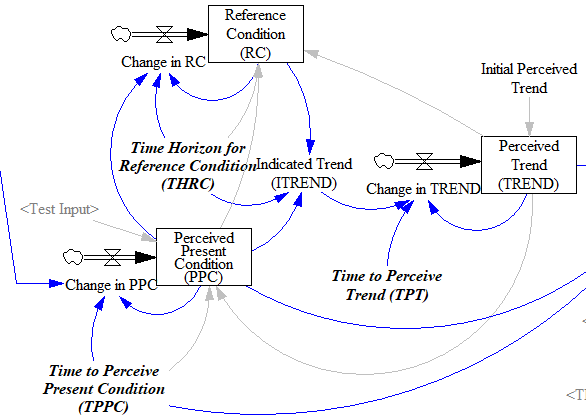
خوشبختانه، توابع ساده قابل ذخیره هستند. در “شکل‌گیری انتظارات در مدل‌های شبیه‌سازی رفتاری“، جان استرمن یک تابع TREND مرتبه سوم جایگزین را توصیف می‌کند که استحکام و واقع‌گرایی را بهبود می‌بخشد. همین ساختار را می‌توان در بحث عالی انتظارات در پویایی کسب و کار، فصل 16 یافت.

من جزئیات را به مقاله واگذار می‌کنم، اما روش اساسی به این صورت است:

• تشخیص دهید که ورودی به طور آنی درک نمی‌شود، بلکه فقط پس از مدتی تأخیر (که با هموارسازی نشان داده می‌شود) درک می‌شود. این ممکن است این واقعیت را نشان دهد که روش‌های حسابداری رسمی فقط نتایج را با تأخیر گزارش می‌کنند، یا اینکه شما فقط قیمت پنیر را در سوپرمارکت به طور متناوب می‌بینید.
• یک نقطه تاریخی (شرایط مرجع) را با هموارسازی، مانند روش‌های ساده‌تر، ردیابی کنید.
• روند نشان داده شده را به عنوان شیب کسری بین شرایط حال حاضر درک شده و شرایط مرجع اندازه‌گیری کنید.
• روند نشان داده شده را دوباره هموار کنید تا روند درک شده نهایی را تشکیل دهید. هموارسازی از تغییرات ناگهانی در روند نشان داده شده جلوگیری می‌کند که باعث بیش از حد یا کمتر از حد در تخمین روند و برون‌یابی‌هایی که از آن استفاده می‌کنند، شود.

یک مورد میانی وجود دارد که در واقع چیزی است که من به احتمال زیاد زمانی که به چیزی شبیه این نیاز دارم به آن می‌رسم: هموارسازی مرتبه دوم. در واقع چندین رویکرد بسیار مشابه (به عنوان مثال، هموارسازی نمایی مضاعف را ببینید) در ادبیات آماری وجود دارد. باید کمی محتاط باشید، زیرا اینها اغلب در زمان گسسته بیان می‌شوند و بنابراین برای انطباق با زمان پیوسته و/یا فواصل داده‌های ناهموار نیاز به کمی فکر دارند.

نسخه‌ای که من استفاده می‌کنم موارد زیر را انجام می‌دهد:

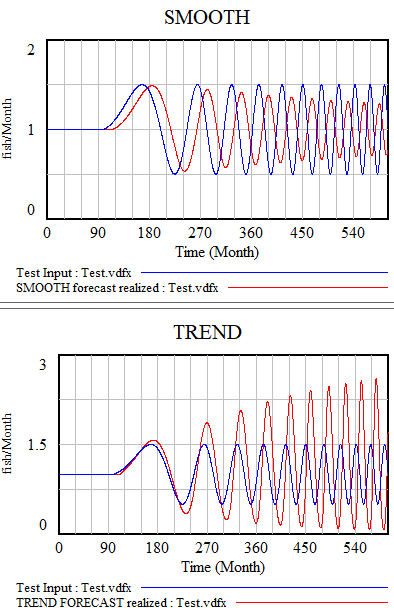
(4) smoothed input = SMOOTH( input, smoothing time )
(5) linear trend = (input-smoothed input) / smoothing time
(6) smoothed trend = SMOOTH( linear trend, trend smoothing time )
(7) forecast = smoothed input + smoothed trend*(smoothing time + forecast horizon)

این بیشتر آنچه را که در یک روش برون‌یابی ساده می‌خواهید، ارائه می‌دهد. تا حد زیادی اختلال PULSE را نادیده می‌گیرد. هنگام ارائه ورودی STEP، بیش از حد ملایم است (تا زمانی که زمان هموارسازی به اندازه کافی طولانی باشد). تا حد زیادی نویز را رد می‌کند، اما همچنان یک RAMP واقعی را به دقت ردیابی می‌کند.

 

بازگشت به رگرسیون

مدل‌های SD معمولاً از رگرسیون خطی اجتناب می‌کنند، به دلایلی که تا حدی مشروع هستند (همانطور که در بالا ذکر شد). اما تا حدی نیز فرهنگی است، به عنوان واکنشی به رگرسیون‌های فوق‌العاده احمقانه‌ای که در زمان پیدایش SD به عنوان مدل در سایر زمینه‌ها پذیرفته می‌شد. نباید کودک را با آب حمام بیرون بریزیم.

خوشبختانه، در حالی که اکثر نرم‌افزارها رگرسیون خطی را به طور خاص در دسترس قرار نمی‌دهند، معلوم می‌شود که پیاده‌سازی یک الگوریتم رگرسیون آنلاین با انبارها و جریان‌ها بدون نیاز به ذخیره بردارهای داده آسان است. بینش اساسی این است که شیب رگرسیون (که معمولاً بتا نامیده می‌شود) توسط:

(8) slope = covar(x,y) / var(x)

داده می‌شود، جایی که x زمان و y ورودی برای پیش‌بینی است. اما var() و covar() فقط مجموع مربع‌ها و ضرب‌های متقابل هستند. اگر با داشتن وزن‌دهی نمایی رگرسیون موافق باشیم، که داده‌های جدیدتر را ترجیح می‌دهد، می‌توانیم اینها را به عنوان مجموع‌های متحرک (مشابه SMOOTHها) ردیابی کنیم. به عنوان یک ساده‌سازی بیشتر، تا زمانی که پنجره هموارسازی در حال تغییر نیست، می‌توانیم var(x) را مستقیماً از پنجره هموارسازی محاسبه کنیم، بنابراین فقط باید میانگین و کوواریانس را ردیابی کنیم، که یک رویکرد هموارسازی مرتبه دوم دیگر را به دست می‌دهد.

اگر تصمیم‌گیرندگان واقعی که الهام‌بخش مدل شما هستند در واقع از رگرسیون خطی استفاده می‌کنند، این ممکن است روش مفیدی برای پیاده‌سازی آن باشد. در صورت نیاز، پیاده‌سازی می‌تواند به وزن‌دهی مساوی در یک بازه محدود گسترش یابد. من رویکرد هموارسازی مرتبه دوم را شهودی‌تر می‌دانم و به همان اندازه خوب عمل می‌کند، بنابراین تمایل دارم در اکثر موارد آن را ترجیح دهم.

 

افزونه‌ها

بیشتر آنچه در بالا توضیح دادم خطی است، یعنی رشد یا کاهش خطی کمیت مورد نظر را فرض می‌کند. برای بسیاری از موارد، رشد نمایی نمایش بهتری خواهد بود. معادلات (3) و (3b) این را فرض می‌کنند، اما هر یک از روش‌های دیگر را می‌توان با عمل کردن بر روی لگاریتم ورودی و سپس معکوس کردن آن با exp(…) برای تشکیل خروجی نهایی، برای فرض رفتار نمایی تطبیق داد.

همه مدل‌های توضیح داده شده در اینجا یک ضعف مشترک دارند: ورودی‌های چرخه‌ای.

هنگام ارائه یک موج سینوسی، ساده‌ترین رویکرد – هموارسازی – فقط با بولدوزر از آن عبور می‌کند. هر چه فرکانس بالاتر باشد، سیگنال کمتری به پیش‌بینی منتقل می‌شود. تابع TREND می‌تواند یک موج را دنبال کند اگر دوره طولانی‌تر از زمان هموارسازی باشد. اگر پویایی‌ها سریع‌تر باشند، شروع به از دست دادن نقاط عطف و بیش از حد چشمگیر می‌کند. روش‌های مرتبه بالاتر بهتر هستند، اما هنوز واقعاً رضایت‌بخش نیستند. نکته اصلی این است که روش پیش‌بینی شما باید از مدلی استفاده کند که قادر به نمایش سیگنال باشد و هیچ یک از روش‌های بالا چیزی در مورد رفتار چرخه‌ای نشان نمی‌دهند.

رویکردهای آماری زیادی برای تشخیص فصلی بودن وجود دارد که می‌توانید در گوگل جستجو کنید. بسیاری از آنها شامل تکنیک‌های طبقه‌بندی هستند، مشابه آنچه در ضمیمه N پویایی صنعتی، چرخه‌های فصلی خود تولید شده توضیح داده شده است.

 

مدل

مدل Vensim، با فایل‌های تغییرات (.cin) که برخی از آزمایش‌های مختلف را پیاده‌سازی می‌کنند، پس از خرید، قابل دانلود است.

من این را در DSS توسعه دادم و قبل از بارگذاری فراموش کردم PLE را آزمایش کنم. اگر مشکلی دارید، لطفاً نظر دهید تا آن را برای کار کردن تطبیق دهم.

یک نسخه Ventity در راه است.