مراقب تفسیر R0 و مدل‌هایی باشید که یک R0 تخمین زده شده در یک زمینه را به ساختار تأخیر از زمینه دیگر متصل می‌کنند.
این پست در ابتدا به عنوان یک پست فنی در مورد مدلهای عفونت برای متخصصان SD علاقه‌مند به اپیدمیولوژی شروع شد. با این حال، به موضوع مهم‌تری برای سیاست‌های مربوط به ویروس کرونا تبدیل شده است.
این موضوع با یک معما آغاز شد: من مدل مفهومی ویروس کرونا خود را برای مناطق متعدد دوباره پیاده‌سازی کردم و آن را برای ایتالیا و سوئیس تنظیم کردم. هدف استفاده از آن برای بررسی سیاست‌های بستن مرز بود. اما کالیبراسیون مشکلی را آشکار کرد: استفاده از پارامترهای اصلی برای زمان نهفتگی، زمان بهبودی و R0 رشد ملایمی در عفونت‌ها ایجاد کرد. تنظیم مجدد برای مطابقت با داده‌ها R0=5 را به دست می‌دهد که خارج از محدوده اکثر تخمین‌ها است. همچنین کنترل را بسیار دشوار می‌کند، زیرا باید انتقال را 1-1/R0 = 80٪ کاهش دهید تا از گسترش آن جلوگیری کنید.
برای درک دلیل آن، تصمیم گرفتم مدل را به صورت تحلیلی برای نرخ رشد حالت پایدار در دوره عفونت اولیه حل کنم، زمانی که افراد مستعد زیادی وجود دارند، بنابراین نرخ عفونت با در دسترس بودن قربانیان محدود نمی‌شود. این تحلیل در بخش‌های بعدی بازتولید شده است. این موضوع به عنوان روشی برای تفکر در مورد رشد در مدلهای SD، نه تنها برای همه‌گیری‌ها، بلکه در بازاریابی (مدل انتشار باس اساساً یک مدل همه‌گیری است) و در اقتصادها و زنجیره‌های تأمین در حال رشد، مورد توجه عمومی است.
با این حال، ابتدا به اصل مطلب می‌پردازم.
معما وجود دارد زیرا R0 توصیف کاملی از ساختار یک همه‌گیری نیست. این موضوع برخی از موارد مهم در مورد نحوه آشکار شدن آن را به شما می‌گوید، مانند اینکه برای متوقف کردن آن چقدر باید انتقال را کاهش دهید، اما به طور مهم، سرعت آن را نمی‌گوید. دلیل آن این است که نرخ رشد با زمان نهفتگی و بهبودی، یا به طور کلی‌تر، توزیع زمان تولید (زمان بین عفونت‌های اولیه و ثانویه) درگیر است.
این بدان معناست که یک مقدار R0 تخمین زده شده با یک مجموعه فرضیات در مورد زمان تولید (به عنوان مثال، با استفاده از بسته R R0) را نمی‌توان بدون تغییر مسیر همه‌گیری، به یک مدل SEIR با فرضیات ساختار تأخیر متفاوت متصل کرد. به طور خاص، نرخ رشد احتمالاً متفاوت خواهد بود. متأسفانه، نرخ رشد بسیار مهم است، زیرا بر زمانی تأثیر می‌گذارد که آستانه‌های بحرانی مانند ظرفیت دستگاه تنفس نقض می‌شوند.
ریاضیات این موضوع به وضوح توسط Wallinga & Lipsitch بیان شده است. آنها به این مسئله از توابع مولد نزدیک می‌شوند، که راه‌حل‌های بسته ساده را کمی راحت‌تر از محاسبات رشد حالت پایدار من در زیر ارائه می‌دهند. به عنوان مثال، برای مدل SEIR،
R0 = (1 + r/b1)(1 + r/b2) (Eqn. 3.2)
جایی که r نرخ رشد، b1 معکوس زمان نهفتگی و b2 معکوس زمان بهبودی است. اگر r = 0.3/روز، b1 = 1/(5 روز)، b2 = 1/(10 روز) را وارد کنید، R0 = 10 می‌شود، که برای COVID-19 قابل قبول نیست. به طور مشابه، اگر R0=2.4 را که اغلب دیده می‌شود با ثابت‌های زمانی بالا وارد کنید، رشد 8٪ در روز را به دست می‌آورید، نه 30٪ در روز مشاهده شده.
در واقع، راه‌های بیشتری برای ایجاد مشکل با استفاده از R0 به عنوان یک میانبر برای فرضیات غنی در مدل‌ها وجود دارد. پویایی تصادفی و توپولوژی شبکه، برای مثال، مهم هستند. در مقاله Li Blakely & Smith خطای R0 می‌نویسند،
با این حال، تقریباً در هر جنبه‌ای که مهم است، R0 ناقص است. بیماری‌ها می‌توانند با R0 < 1 پایدار بمانند، در حالی که بیماری‌هایی با R0 > 1 می‌توانند از بین بروند. ما نشان می‌دهیم که همان مدل مالاریا بسته به روش مورد استفاده، مقادیر مختلف R0 را به دست می‌دهد، با تنها ویژگی مشترک اینکه آستانه‌ای در 1 دارند. ما همچنین مقادیر تخمین زده شده R0 را برای انواع بیماری‌ها بررسی می‌کنیم و برخی از جایگزین‌های پیشنهادی را بررسی می‌کنیم. اگر قرار است از R0 استفاده شود، باید با هشدارهایی در مورد روش محاسبه، فرضیات مدل اساسی و شواهدی مبنی بر اینکه واقعاً یک آستانه است، همراه باشد. در غیر این صورت، مفهوم بی‌معنی است.
آیا این صرفاً یک مشکل نظری است؟ فکر نمی‌کنم. در اینجا وضعیت برخی از شبیه‌سازهای آنلاین نوع SEIR آمده است:
| Model | R0 (dmnl) | Incubation (days) | Infectious (days) | Growth Rate (%/day) |
| My original | 3.3 | 5 | 7 | 17 |
| Homer US | 3.5 | 5.4 | 11 | 18 |
| covidsim.eu | 4 | 4 & 1 | 10 | 17 |
| Epidemic Calculator | 2.2 | 5.2 | 2.9 | 30* |
| Imperial College | 2.4 | 5.1 | ~3** | 20*** |
*مشاهده شده در شبیه‌ساز؛ با محاسبه حالت پایدار مطابقت ندارد، بنابراین برخی از ویژگی‌ها ناشناخته هستند.
**تخمین زده شده از میانگین زمان تولید 6.5 روزه، توزیع شده در اطراف زمان نهفتگی.
***گزارش نشده است؛ زمان دو برابر شدن حدود 6 روز به نظر می‌رسد.
فکر می‌کنم این قطعاً یک وضعیت برج بابل است. به نظر می‌رسد که ساختار سنی مرتبه پایین در مدل SEIR برای نمایش دقیق پویایی‌ها مشکل‌ساز است. اما به نظر می‌رسد که انتخاب پارامتر قطعه‌ای عدم قطعیت واقعی در این مقادیر را دست کم می‌گیرد. ما باید توزیع مشترک R0 و توزیع زمان تولید را بدانیم تا بتوانیم آنچه را که در حال رخ دادن است به درستی نشان دهیم.
رشد حالت پایدار – SIR
مدل همه‌گیری کلاسیک مدل SIR است:
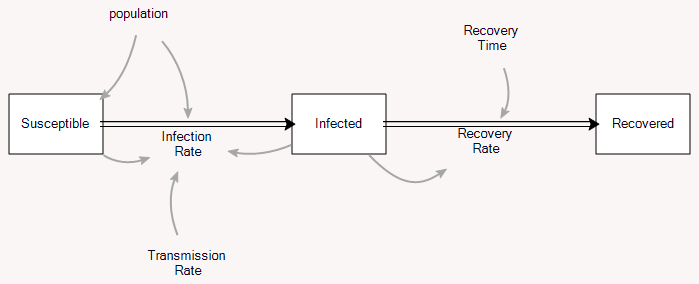
تحلیل کامل پیچیده است، اما اصل مطلب بسیار ساده است. (یک تحلیل فضای فاز جالب در اینجا وجود دارد و مقاله اصلی Kormack & McKendrick در اینجا است. آموزش Vensim من در اینجا است.) با فکر کردن به مدل از دیدگاه SD، به رابطه بین رشد حالت پایدار عفونت‌ها در اوایل همه‌گیری و نسبت تولید مثل R0 علاقه‌مند شدم.
موارد زیر این محاسبه را گام به گام توضیح می‌دهد. همان ریاضیات اغلب در تنظیمات دیگر مفید است. به عنوان مثال، اگر زنجیره تأمینی در یک اقتصاد در حال رشد دارید، مقداردهی اولیه همه انبارها به همان مسیر رشد مفید است.
جریان کلیدی در مدل عفونت‌ها است:
عفونی کردن = نرخ انتقال * عفونی * مستعد / جمعیت
با واحدها:
people/day = (people/person)/day * people *people / people
نرخ انتقال احتمال انتقال بیماری از یک نفر به نفر دیگر را خلاصه می‌کند: افراد چند بار در تماس هستند و احتمال انتقال در نتیجه تماس چقدر است.
سپس انبار افراد عفونی مطابق با موارد زیر تغییر می‌کند:
d(Infected)/dt = Infecting - Recovering = Transmission Rate * Infected * Susceptible / Population - Infected / Duration
d(عفونی)/dt = عفونی کردن - بهبودی = نرخ انتقال * عفونی * مستعد / جمعیت - عفونی / مدت زمان
در اوایل همه‌گیری، مستعد / جمعیت تقریباً 1 است، بنابراین این ساده می‌شود به
= Infected * ( Transmission Rate - 1/Duration )
بنابراین در ابتدا، همه‌گیری با نرخ
g = Transmission Rate - 1/Duration ~ fraction/day
این موضوع ارتباط نزدیکی با نسبت تولید مثل، R0 دارد،
Transmission Rate = R0/Duration g = (R0-1)/Duration
بنابراین g = 0 زمانی که نرخ انتقال = 1/مدت زمان و زمانی که R0 = 1 است.
با تنظیم مجدد،
R0 = 1 + g*Duration R0 = 1 + g/Removal Rate Removal Rate = 1/Duration
SEIR
تا اینجا خوب است. اما ویروس کرونا بلافاصله عفونی نیست، بنابراین بهتر است با مدل SEIR نشان داده شود:
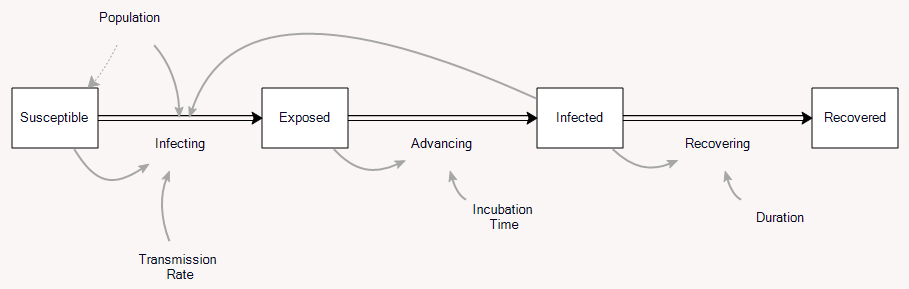
این یک انبار افراد در معرض را اضافه می‌کند، که هنوز علائم ندارند و (به اندازه) دیگران عفونی نیستند. بنابراین این موضوع ما را به سؤالی می‌رساند که در ابتدا به آن علاقه‌مند بودم: چگونه تأخیر بین عفونت و عفونی بودن رشد بیماری را تغییر می‌دهد؟ این فقط جبر است، اما معلوم می‌شود که کمی آشفته است.
باز هم، از آنجایی که فقط به همه‌گیری اولیه علاقه‌مندیم، مستعد و بهبود یافته را نادیده می‌گیریم و فقط در معرض E و عفونی I را در نظر می‌گیریم. نرخ‌های عفونی کردن، پیشرفت و بهبودی را به ترتیب i، a و r می‌نامیم. زمان نهفتگی را Te و مدت زمان عفونت را Ti و نرخ انتقال را بتا (معمولاً β نامیده می‌شود، اما من وقت حروف یونانی را ندارم) می‌نامیم. افراد در معرض تا حدی عفونی هستند (در نمودار بالا نشان داده نشده است)، به طوری که
i = beta*(I + alpha*E)
در حالت پایدار، هر دو انبار با نرخ g یکسان رشد می‌کنند:
g = dE/E = dI/I (i-a)/E = (a-r)/I (beta*(I+alpha*E)-E/Te)/E = (E/Te-I/Ti)/I
این را برای
x = I/E = [-(beta*alpha*te+te/ti-1)+SQRT( (beta*alpha*te+te/ti-1)^2
+ 4*beta*te )]/(2*beta*te)
حل می‌کنیم.
سپس یک محدودیت دیگر وجود دارد: مجموع I + E باید با همان نرخ کسری اجزای منفرد رشد کند.
g = d(E+I)/(E+I) = (b(I+alpha*E) - I/Ti)/(E+I)
با جایگزینی E= I/x،
g = (beta*(1+alpha/x)-1/ti)/(1/x+1)
همه اینها در مدل آمده است. کافی است خرید کنید.
بخش بالایی نشان می‌دهد که چگونه مقادیر مشاهده شده (“متغیرهای obs”) به سرعت به مقادیر مورد انتظار (“* متغیرها”) برای نرخ رشد و نسبت I/E همگرا می‌شوند:
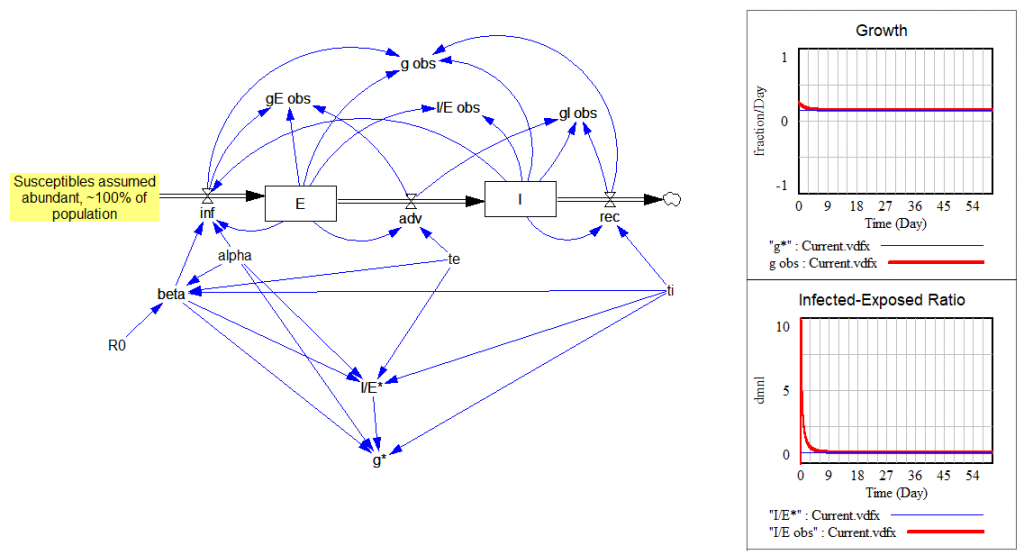بخش پایین‌تر یک کپی از همان ساختار است، که بازخورد از E و I به عفونت‌ها را قطع می‌کند. در عوض، من یک تکانه واحد از عفونت‌ها را وارد می‌کنم (یعنی یک عفونت در زمان نزدیک به 0). سپس عفونت‌هایی را که آن شخص در طول دوره حضور خود در سیستم ایجاد می‌کند، محاسبه می‌کنم. این باید به R0 همگرا شود:
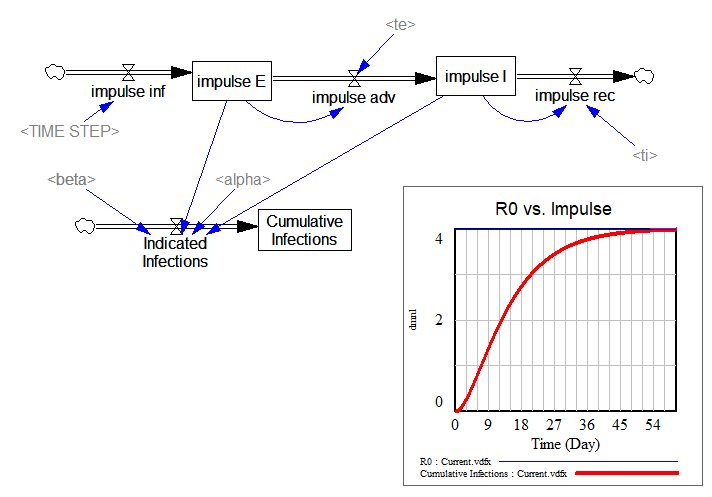
… و همگرا می‌شود.
متوجه خواهید شد که اکنون چندین بررسی متقابل برای این نتایج دارم: راه‌حل‌های تحلیلی در مقایسه با شبیه‌سازی‌ها، و پاسخ ضربه که نتایج حلقه بسته را تأیید می‌کند. این ممکن است برای افرادی که اشتباه نمی‌کنند زیاده‌روی باشد، اما برای من اینطور نیست. من نمی‌خواهم سرنوشت خود را به افرادی بسپارم که فکر می‌کنند اشتباه نمی‌کنند. یک نفر از 100 نفر ممکن است نابغه باشد، اما 99 نفر دیگر فقط متعصبان متکبر هستند. به همین دلیل است که من همیشه امیدوارم بین شبیه‌سازی‌ها، راه‌حل‌های تحلیلی و داده‌ها، مثلث‌بندی انجام شود.
