من در یک بسته یادگیری ماشین به قواعد نلسون برخورد کردم. اینها مجموعهای از روشهای ابتکاری برای تشخیص تغییرات در کنترل فرآیند آماری هستند. گنجاندن آنها کمی شبیه به هدایت یک 787 با یک رایانه پرواز مکانیکی بود (که اتفاقاً دستگاه بسیار جالبی است).
ایده بسیار ساده است. شما یک سری زمانی از اندازهگیریها را دارید که به نمرات Z نرمال شدهاند، و بنابراین (بیشتر اوقات) با مثبت یا منفی 3 انحراف استاندارد تغییر میکنند. قواعد نلسون راهی برای تشخیص ناهنجاریها ارائه میدهند: انحراف، نوسان، واریانس بالا یا پایین و غیره. به عنوان مثال، قاعده 1 فقط یک آستانه برای تشخیص نقاط پرت است: هر زمان که اندازهگیری بیش از 3 SD از میانگین باشد، فعال میشود.
در زمینه یادگیری ماشین، برای من عجیب است که از این روشهای ابتکاری زمانی که آزمایشهای قدرتمندتری در دسترس هستند استفاده کنم. این شبیه به مشکل تصمیمگیری در مورد اینکه آیا یک مولد اعداد تصادفی واقعاً تصادفی است یا خیر، است. تعیین اینکه آیا توزیع یکنواخت مقادیر را تولید میکند یا خیر، نسبتاً آسان است، اما در مورد چرخهها یا سایر الگوهای بلند مدت چه؟ وقتی RNG را در Vensim جایگزین کردیم، زمان زیادی را صرف کار روی این موضوع کردم. بسیاری از آزمایشهای استاندارد در دسترس هستند. همه آنها مستقیماً قابل اجرا نیستند، اما تفکر در مورد آنها مفید است.
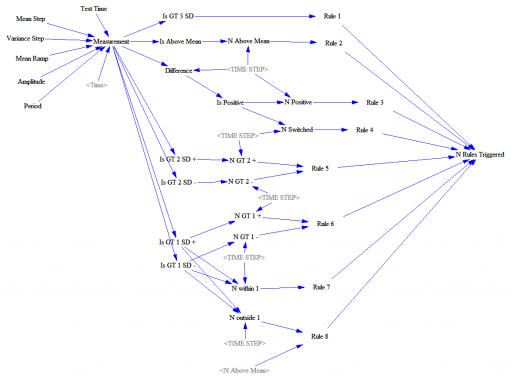
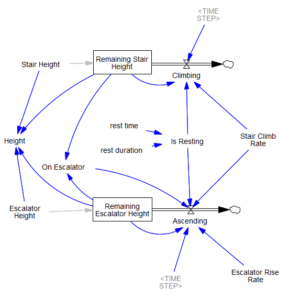
در هر صورت، من کنجکاو شدم که قواعد نلسون در دنیای واقعی چگونه عمل میکنند، بنابراین یک مدل آزمایشی توسعه دادم.
این یک ورودی آزمایشی (مقادیر تصادفی با توزیع نرمال، با یک سیگنال اختیاری که روی آن قرار گرفته است) را به مجموعهای از متغیرهای حسابداری که معیارها را ردیابی میکنند و با آستانههای قاعده مقایسه میکنند، تغذیه میکند. برخی از اینها پیچیده هستند.
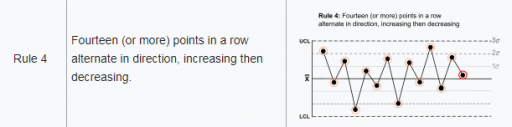
به عنوان مثال، قاعده 4 به دنبال 14 نقطه با تفاوتهای متناوب است. ردیابی آن در Vensim، جایی که معمولاً بیشتر به زمان پیوسته علاقهمند هستیم، کمی دشوار است. من با ساختار زیر به این موضوع میپردازم:
Difference = Measurement-SMOOTH(Measurement,TIME STEP)
**************************************************************
Is Positive=IF THEN ELSE(Difference>0,1,-1)
**************************************************************
N Switched=INTEG(IF THEN ELSE(Is Positive>0 :AND: N Switched<0
,(1-2*N Switched )/TIME STEP
,IF THEN ELSE(Is Positive<0 :AND: N Switched>0
,(-1-2*N Switched)/TIME STEP
,(Is Positive-N Switched)/TIME STEP)),0)
**************************************************************
Rule 4=IF THEN ELSE(ABS(N Switched)>14,1,0)
**************************************************************
در اینجا یک ترفند وجود دارد. برای شمارش تفاوتهای متناوب، باید (الف) شمارش قبلی و (ب) اینکه آیا تفاوت قبلی مثبت یا منفی بوده است را بدانیم. در بالا، N Switched هر دو قسمت اطلاعات را در یک انبار واحد (INTEG) ذخیره میکند. این امکانپذیر است زیرا شمارش گسسته و مثبت است، بنابراین میتوانیم با دادن علامت تفاوت قبلی که با آن مواجه شدهایم، فضای ذخیرهسازی را بیش از حد بارگذاری کنیم.
بنابراین، اگر تفاوت فعلی منفی باشد (Is Positive < 0) و تفاوت قبلی مثبت باشد (N Switched > 0)، ما (الف) با کم کردن 2*N Switched علامت شمارش را معکوس میکنیم، و (ب) شمارش را افزایش میدهیم، در اینجا با کم کردن 1 برای منفیتر کردن آن.
ترفندهای مشابهی در جاهای دیگر ساختار استفاده میشود.
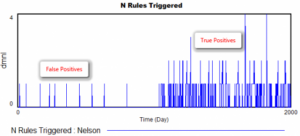
عملکرد آن چگونه است؟ به طرز شگفت انگیزی خوب. در اینجا اتفاقی میافتد که توزیع اندازهگیری در نیمه راه شبیهسازی به اندازه یک انحراف استاندارد تغییر میکند:
در 1000 روز اول چند مثبت کاذب وجود دارد، اما پس از تغییر، تشخیصهای بسیار بیشتری از قواعد متعدد وجود دارد.
قواعد در تشخیص انواع آسیبشناسیها بسیار خوب هستند: افزایش یا کاهش واریانس، تغییر در میانگین، روند و نوسانات. قواعد همچنین نرخهای مثبت کاذب متفاوتی دارند، که ممکن است خوب باشد، تا زمانی که مشکلات غیر همپوشانی را تشخیص دهند، و تفاوتهای بزرگی در حساسیت نیز نداشته باشند. (مقاله اصلی ممکن است چیزهای بیشتری در مورد این موضوع داشته باشد – من بررسی نکردهام.)
با این حال، من کاملاً مطمئن هستم که میتوانم برخی از ورودیهای آسیبشناختی را توسعه دهم که از این قواعد عبور کنند. در مقابل، من کاملاً مطمئن هستم که برای عبور دادن چیزی از مجموعههای آزمایشی NIST یا Diehard RNG با مشکل مواجه خواهم شد.
اگر این را از ابتدا طراحی میکردم، از ابزارهای یادگیری ماشین به طور مستقیمتر استفاده میکردم – آزمایشهای زیادی برای توزیعها، تغییرات، شکستهای روند، نوسان و غیره وجود دارد که میتوان به صورت آنلاین با تفسیر احتمال سازگار و معاوضههای مثبت/منفی کاذب بهینه استفاده کرد.
در اینجا مدل آمده است: