ماجراجویی‌های ناگوار با قانون لیتل – مدل ونسیم

من روی یک مدل ناوگان وسایل نقلیه کار می‌کردم، و یک صفحه گسترده را با استفاده از گروه‌های هم‌نسل پویا در Ventity بازسازی می‌کردم.

طول عمر وسیله نقلیه در صفحه گسترده 11 سال است و گسسته است. این بدان معناست که هر وسیله نقلیه دقیقاً 11 سال پس از ورود به سرویس بازنشسته می‌شود. این موضوع برای من یک هشدار قرمز ایجاد کرد، زیرا نشان دهنده طول عمر نسبتاً کوتاه وسیله نقلیه است. من از کار در حوزه‌های قضایی دیگر می‌دانم که میانگین عمر یک وسیله نقلیه معمولاً بیشتر شبیه 16-18 سال است (و با بهبود کیفیت، طولانی‌تر می‌شود).

بنابراین، رقم 11 سال از کجا می‌آید؟ ما مطمئن نیستیم. سایر داده‌های منتشر شده برای منطقه میانگین سن وسیله نقلیه 8.5 سال را نشان می‌دهد، بنابراین اینطور نیست. یکی از همکاران Ventana اشاره کرد که ممکن است یک تخمین حالت پایدار از ترکیب داده‌های ناوگان وسایل نقلیه با داده‌های فروش وسایل نقلیه جدید باشد:

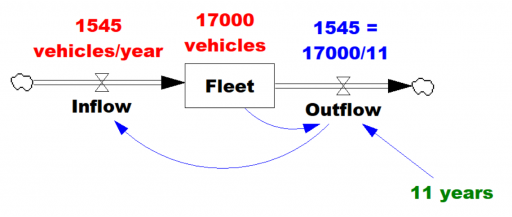
با توجه به داده‌ها (قرمز)، فرض کنید که موجودی وسایل نقلیه در تعادل است (ورودی=خروجی). سپس از قانون لیتل نتیجه می‌شود که میانگین طول عمر وسایل نقلیه باید 11 سال باشد. قانون لیتل بدون توجه به توزیع تأخیر، یعنی بدون توجه به مرتبه تأخیر، کار می‌کند، اما اگر ناوگان را به عنوان یک سیستم مرتبه اول فرمول‌بندی می‌کردید، دقیقاً نحوه نوشتن معادله خروجی به این صورت بود: خروجی = ناوگان/طول عمر، با طول عمر=11 سال.

… میانگین بلندمدت تعداد L مشتریان در یک سیستم ثابت برابر است با میانگین بلندمدت نرخ ورود مؤثر λ ضربدر میانگین زمان W که یک مشتری در سیستم صرف می‌کند. – ویکی‌پدیا

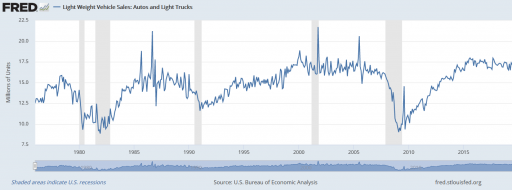
با این حال، در اینجا خطری وجود دارد. ممکن است سیستم در تعادل نباشد. سپس هم فرض ورودی=خروجی و هم ایستایی مورد نیاز در قانون لیتل نقض می‌شود. متأسفانه، فروش وسایل نقلیه نسبتاً ناپایدار است، به ویژه در اطراف رویدادهایی مانند رکود سال 2008:

استفاده از میانگین سن وسایل نقلیه به عنوان یک نقطه داده دیگر وسوسه‌انگیز است، اما معلوم می‌شود که ایده بدی است. میانگین سن وسایل نقلیه هم به تغییرات در ورودی و هم به توزیع فرض شده فرآیند دور ریز حساس است. مدل Ventity زیر این مشکل را با استفاده از برخی از همان مکانیزم‌های مدل ارلانگ هفته گذشته نشان می‌دهد.

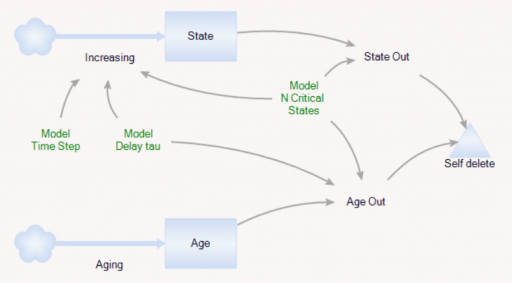
مانند قبل، جمعیتی از موجودیت‌ها (عامل=agent) وجود دارد. هر کدام دارای آبشاری از N حالت داخلی هستند که توسط یک شمارنده انبار و سنی که به طور مداوم افزایش می‌یابد، نشان داده می‌شوند. یک موجودیت زمانی خود را حذف می‌کند که خیلی پیر باشد یا تعداد حالت آن خیلی زیاد باشد.

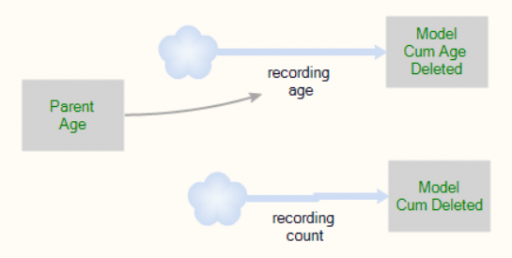
برای اهداف حسابداری، هنگامی که یک موجودیت “می‌میرد”، رویداد را با افزایش شمارنده‌های انبار در موجودیت مدل ثبت می‌کند:

به این ترتیب، می‌توانیم پیگیری کنیم که میانگین سن موجودیت در زمان حذف خود چقدر بوده است. این باید میانگین زمان اقامت در قانون لیتل باشد. همچنین می‌توانیم میانگین سن موجودیت‌های موجود را پیگیری کنیم تا ببینیم آیا یکسان است یا خیر.

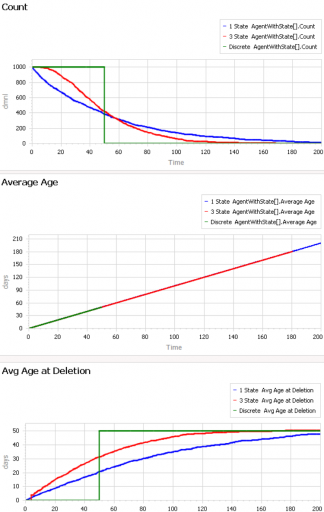
ابتدا یک مورد خاص بسیار ساده و بسیار غیر ثابت را در نظر بگیرید که در آن هیچ جریان گردش موجودیت وجود ندارد. فقط یک جمعیت اولیه از موجودیت‌هایی با سن 0 وجود دارد که به تدریج سیستم را ترک می‌کنند. در اینجا سه نوع از آن آزمایش وجود دارد:

Model.Delay tau = 50 و Model.Flow Start Time = 1000 را تنظیم کنید تا این آزمایش را تکرار کنید.

خط آبی آنالوگ جمعیت تصادفی تأخیر مرتبه اول کلاسیک است. احتمال خروج یک موجودیت معین در طول زمان ثابت است، مانند واپاشی رادیواکتیو. بنابراین ما واپاشی نمایی را با تعداد = N0*exp(-زمان/تأخیر tau) دریافت می‌کنیم. خط قرمز معادل مرتبه سوم است که توزیع ارلانگ 3 را به دست می‌دهد. خط سبز معادل تأخیر خط لوله است که در آن همه موجودیت‌ها در یک سن مشخص خود حذف می‌شوند، نه با یک توزیع تصادفی. بنابراین جمعیت در زمان 50 از 1000 به 0 می‌رسد.

دو پنل پایین میانگین سن موجودیت‌های بازمانده (وسط) را با میانگین سنی که موجودیت‌ها خود حذف می‌کنند (پایین) مقایسه می‌کنند. در پایین، می‌توانید ببینید که همه انواع در نهایت به (تقریباً) طول عمر مورد انتظار 50 ساله موجودیت همگرا می‌شوند. با این حال، هر مسیر در ابتدا طول عمر کوتاه‌تری را نشان می‌دهد. این به دلیل نوعی سوگیری سانسور است – در یک نقطه معین در زمان، طولانی‌ترین عمر موجودیت‌ها هنوز مشاهده نشده‌اند.

پنل میانی نشان می‌دهد که چگونه میانگین سن می‌تواند گمراه کننده باشد. در این حالت، سن=زمان برای همه موجودیت‌ها است و بنابراین میانگین سن به طور خطی افزایش می‌یابد، حتی اگر زمان اقامت مورد انتظار ثابت باشد.

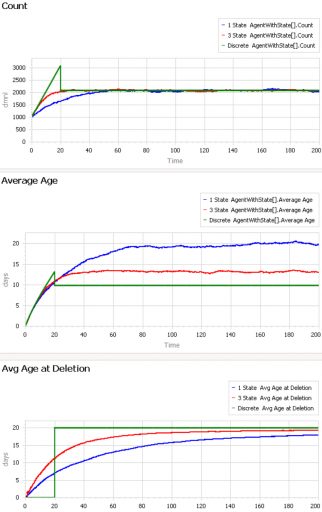
در نقطه مقابل، در اینجا یک آزمایش با جریان ثابت عوامل جدید وجود دارد، به طوری که سیستم پس از چند ثابت زمانی در تعادل است:

Model.Delay tau = 20 و Model.Flow Start Time = 0 را تنظیم کنید تا این آزمایش را تکرار کنید.

پس از اینکه گذرا اولیه از بین رفت (در زمان 20 تا 60)، هر 3 زمان اقامت (سن در حذف) به مقدار مورد انتظار 20 همگرا می‌شوند. اما به سنین توجه کنید. آنها نیز همگرا می‌شوند، اما مقدار به توزیع بستگی دارد. برای سیستم مرتبه اول (آبی)، میانگین سن واقعاً برابر با میانگین زمان اقامت 20 سال است. اما سیستم خط لوله (سبز) میانگین سنی دارد که نصف آن است، 10 سال. این منطقی است، اگر به یک جمعیت تعادلی متشکل از ترکیبی یکنواخت از سنین بین 0 تا 20 سال فکر کنید. سیستم مرتبه سوم بین این دو است.

این رابطه نامشخص بین سن و زمان اقامت به این معنی است که نمی‌توانیم از میانگین سن ناوگان وسایل نقلیه برای تعیین نرخ گردش وسایل نقلیه استفاده کنیم. این بد است، زیرا سن آماری است که محاسبه آن از پایگاه داده ثبت وسایل نقلیه آسان است. برای دانستن بیشتر، باید شروع به استنباط در مورد ورودی‌ها و خروجی‌ها کنیم – اما اگر پوشش داده‌ها با زمان متفاوت باشد، این کار دشوار است. متأسفانه، این عددی است که برای ما اهمیت دارد، زیرا زمان اقامت وسایل نقلیه در سیستم یک عامل مهم در نفوذ آینده فناوری‌های کم کربن است.

مدل پس از خرید قابل دانلود خواهد بود.

از جعبه شن تأخیر می‌توان برای بررسی پدیده‌های مشابه در یک محیط پیوسته، کلی و قطعی استفاده کرد.