مدل پویای سندباکس تاخیری

توضیحات

یک قانون ساده برای تخمین اینکه چه مقدار از ورودی یک تاخیر مرتبه اول به عنوان خروجی منتشر شده است وجود دارد: پس از سه ثابت زمانی، 95%. (این همان قانون تخمین مقدار ماده ای است که به صورت تصاعدی در حال پوسیدگی است – حدود 2/3 بعد از یک عمر، 85٪ بعد از دو، 95٪ بعد از سه، و 99٪ بعد از پنج عمر.)

من اخیراً قوانین سرانگشتی را برای ساختارهای تاخیری دیگر (مرتبه سوم یا بالاتر) می‌خواستم، بنابراین برای خودم یک مدل ساده ساختم تا بازی با تاخیر را تسهیل کنم. از تابع DELAY N Vensim استفاده می کند تا تغییر ترتیب تاخیر را آسان کند.

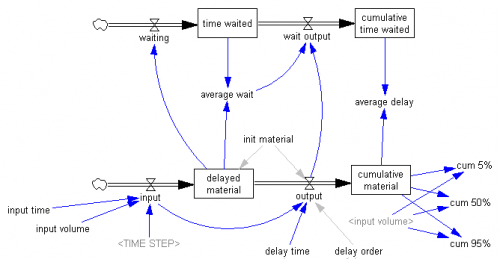
این ساختار است:

ساختار جریان پایین انبار خود تاخیر است. بلند کردن سنگین در واقع در تابع DELAY N در متغیر خروجی است. این تابع در صورت نیاز یک زنجیره پیری مخفی و مرتبه بالاتر ایجاد می کند. پس از آن، موجودی مواد تاخیری فقط یک میانبر حسابداری است که محتویات تمام سهام در زنجیره پنهان را نشان می دهد. ساختار فوقانی برای حسابداری است: این ساختار به طور متوسط ​​مدت زمان باقی مانده در انبار مواد تاخیری را ردیابی می کند و میانگین تاخیر مشاهده شده برای مواد تجمعی که به عنوان خروجی رسیده است را پیگیری می کند.

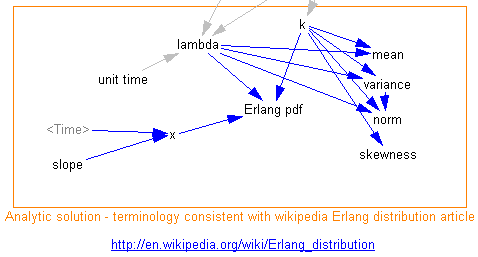
من همچنین ساختار دومی ایجاد کردم که ساختار پویا را به توزیع Erlang مرتبط می کند، همانطور که به راحتی در ویکی پدیا ارائه شده است:من همچنین ساختار دومی ایجاد کردم که ساختار پویا را به توزیع Erlang مرتبط می کند، همانطور که به راحتی در ویکی پدیا ارائه شده است:

این امر تعیین آمار تاخیر یک سفارش را آسان می کند. چیزی که من معمولاً به آن علاقه دارم هنجار است – انحراف استاندارد نرمال شده – یعنی چه تاخیری برای ایجاد پراکندگی مشاهده شده در برخی از فرآیندها لازم است؟ (خوشبختانه، پاسخ اغلب این است که “چه کسی اهمیت می دهد”، اما بهتر است آزمایش کنید تا اینکه نظم دلخواه را به تاخیر بیندازید.)

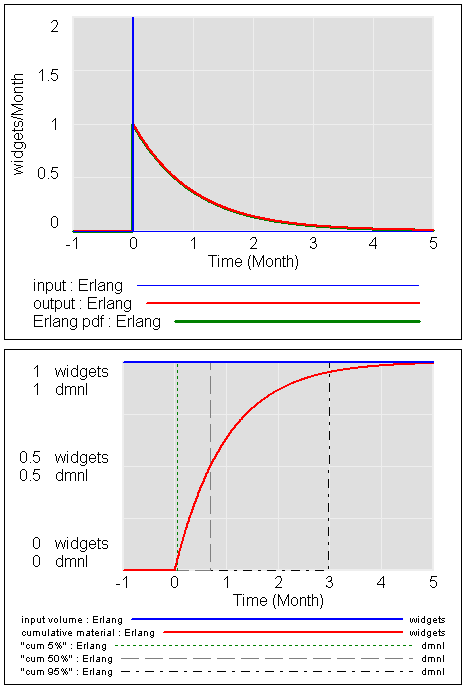
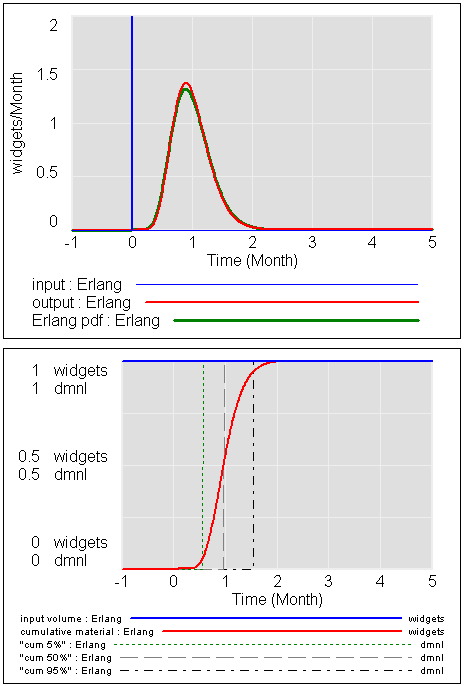
برای تأخیر مرتبه اول وانیلی، می توانید (به سختی) ببینید که توزیع Erlang و رفتار پویا دقیقاً مطابقت دارند.

پانل پایینی نقطه شکست را در 3*tau نشان می دهد (tau = ثابت زمانی = طول عمر = 1 در اینجا) که در آن تاخیر به 95٪ از پاسخ خود رسیده است. همچنین می توانید ببینید که نقطه شکست 50% – نیمه عمر یا میانه تاخیر، در حدود 0.7*tau است. این نقطه ای است که e^(-time/tau)=0.5، یعنی زمان = -ln(0.5)*tau = 0.69 * tau. شما همچنین می توانید ببینید که توزیع بسیار کج است، با تعداد زیادی از افراد اولیه و دم دراز دیرباز – مدل خوبی از زوال تصاعدی، اما نه چندان داغ برای رسیدن پست.پانل پایینی نقطه شکست را در 3*tau نشان می دهد (tau = ثابت زمانی = طول عمر = 1 در اینجا) که در آن تاخیر به 95٪ از پاسخ خود رسیده است. همچنین می توانید ببینید که نقطه شکست 50% – نیمه عمر یا میانه تاخیر، در حدود 0.7*tau است. این نقطه ای است که e^(-time/tau)=0.5، یعنی زمان = -ln(0.5)*tau = 0.69 * tau. شما همچنین می توانید ببینید که توزیع بسیار کج است، با تعداد زیادی از افراد اولیه و دم دراز دیرباز – مدل خوبی از زوال تصاعدی، اما نه چندان داغ برای رسیدن پست.

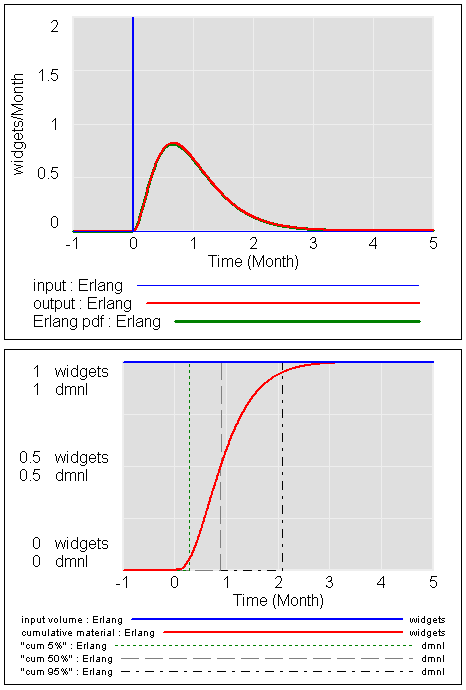
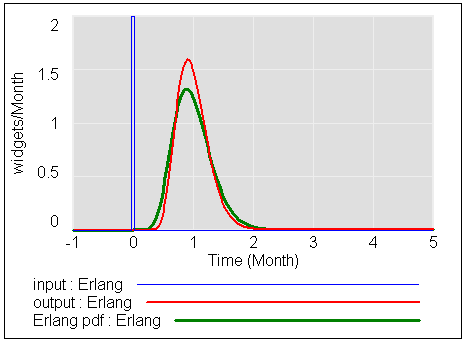
در اینجا تاخیر سفارش سوم است – یک انتخاب رایج:

می بینید که خروجی واریانس کمتری دارد و به ویژه دم سمت راست آنچنان سنگین نیست. 95% از پاسخ ها در 2*tau به جای 3*tau بدست می آید. با وجود چولگی قابل توجه (توجه داشته باشید که حالت هنوز به خوبی در سمت چپ 1*tau است)، 50٪ از پاسخ تقریباً در 1*tau (در واقع 57٪) رخ می دهد.

برای تاخیر سفارش دهم:

اکنون واریانس بسیار کمتر است و توزیع تقریباً متقارن است. پاسخ میانه تقریباً در 1*tau رخ می دهد، همانطور که برای هر تأخیر قابل قبولی در سفارش بالا رخ می دهد. هنجار اکنون 0.3 در مقابل 1 برای نوع اول است، اما هنوز هم بسیار بزرگ است. برای به دست آوردن یک انحراف استاندارد نرمال شده کوچک از یک زنجیره پیری، به یک زنجیره مرتبه بسیار بالا نیاز دارید که معمولاً غیرعملی است زیرا در این صورت هر مرحله از تأخیر دارای یک ثابت زمانی بسیار کوتاه است که به یک TIME STEP کوچک نیاز دارد. مسائل عددی شروع به انباشته شدن می کنند. در اینجا دهمین سفارش تاخیر، با TIME STEP کمی بزرگتر است:

توجه داشته باشید که اکنون خروجی تا حدودی از نتیجه تحلیلی Erlang متفاوت است. این به این دلیل است که تاخیر موثر به طور فزاینده ای گسسته می شود. در این مرحله، اغلب بهتر است به یک تاخیر گسسته مانند DELAY FIXED یا استفاده از یک زنجیره قدیمی صریح با SHIFT IF TRUE تغییر دهید.

می‌توانید درمان کامل‌تری از همه این‌ها را در Steman’s Business Dynamics، بخش‌های 11.2 و 11.7.2-11.7.3 بخوانید.