زمانی که هاستس در سال 2012 ورشکست شد، گمانهزنیهای زیادی در مورد سرنوشت آخرین توینکی وجود داشت، شاید در قفسههای گرد و خاکی یک فروشگاه رفاهی پمپ بنزین در جایی در نیومکزیکو در حال پوسیدن باشد. آیا این ده روز، ده هفته، ده سال طول میکشد؟
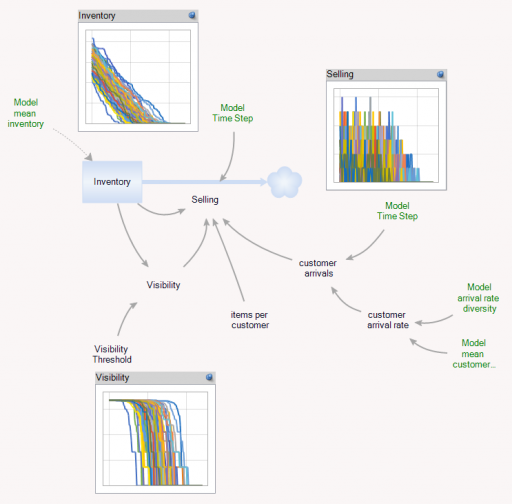
بنابراین، این چه ارتباطی با پویایی سیستم دارد؟ این مسئله مشکل مدلسازی محدودیت موجودی انبار در فروش را به ذهن متبادر میکند. این مشکل به پویایی صنعتی برمیگردد (به متغیر NIR که SSR را هدایت میکند و بحث پیرامون شکلهای 15-5 و 15-7 مراجعه کنید).
اگر فقط یک محصول در یک انبار (یعنی یک فروشگاه) وجود داشته باشد، و دیدهشدن مهم نباشد، محدودیت بسیار ساده است. تا زمانی که یک مورد باقی مانده باشد، فروش یا حمل و نقل میتواند ادامه یابد. محدودیت سپس به این صورت است:
(1) فروش = MIN(فروش مطلوب، موجودی/گام زمانی)
به عبارت دیگر، حداکثر مقداری که در یک گام زمانی میتوان فروخت، مقدار موجودی است که در واقع در دسترس است. به طور کلی، محدودیت به این شکل است:
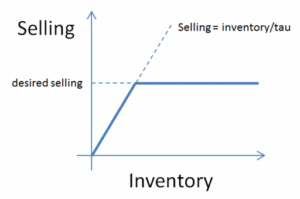
در اینجا، tau یک ثابت زمانی است که میتواند برابر با گام زمانی (DT)، همانطور که در بالا ذکر شد، یا میتواند به یک بازه زمانی طولانیتر تعمیم داده شود که نشاندهنده دستکاری و سایر تأخیرها است.
این را میتوان به نوعی تابع پیوسته تعمیم داد، مانند:
(2) فروش = فروش مطلوب * f(موجودی)
که f() اغلب یک جدول جستجو است. این میتواند کمی دشوار باشد، زیرا باید اطمینان حاصل کنید که f() به اندازه کافی سریع به صفر میرسد تا از محدودیت موجودی/DT بالا پیروی کند.
اما اگر محصولات زیادی و/یا نقاط موجودی زیادی داشته باشید، شاید با نرخ گردش عادی متفاوت؟ چگونه اینها جمع میشوند؟ من مدل اسباببازی زیر را برای یافتن پاسخ ساختم. شما به راحتی میتوانید این کار را در Vensim با آرایهها انجام دهید، اما متوجه شدم که برای Ventity ایدهآل است.
در اینجا تنظیمات آمده است:
ابتدا، مجموعهای از موجودیتهای فروشگاه وجود دارد، که هر کدام دارای موجودی هستند. موجودی اولیه تصادفی است، با توزیع پواسون، که توینکیهای صحیح را تضمین میکند. ورود مشتری نیز دارای توزیع پواسون است، و (به صورت اختیاری) میانگین نرخ ورود در هر فروشگاه متفاوت است. فروش به موجودی موجود از طریق موجودی/DT محدود میشود، و همچنین تحت تأثیر اثر دیدهشدن قرار میگیرد – موجودی قفسه بر احتمال خرید توینکی توسط مشتری تأثیر میگذارد (با توزیع دوجملهای تحقق مییابد). اثر دیدهشدن اشباع میشود، به طوری که بازده افزایشی به اضافه کردن موجودی وجود دارد، همانطور که وقتی موجودی جدید به ردیفهای پشتی قفسه میرود، رخ میدهد.
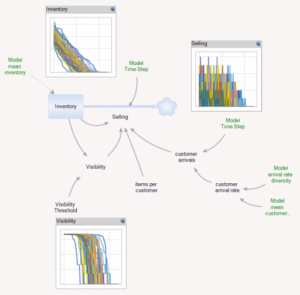
علاوه بر این، یک نوع موجودیت تجمیع وجود دارد، که بسیار شبیه به فروشگاه است، اما قطعی و پیوسته است.
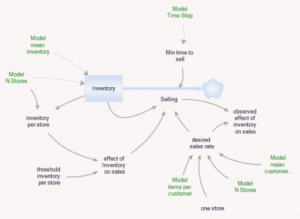
موجودی اولیه و نرخ فروش تجمیع بر روی مقادیر مورد انتظار برای فروشگاههای فردی تنظیم شدهاند. دو نوع محدودیت مختلف بر خروجی موجودی در دسترس است: موجودی/تاو و f(موجودی). نرخ فروش به صورت زیر ساده میشود:
(3) فروش = min(نرخ فروش مطلوب * f(موجودی)، موجودی/حداقل زمان فروش)
(4) حداقل زمان فروش >= گام زمانی
در فروشگاه و تجمیع، اثر غیرخطی موجودی بر فروش (به نام دیدهشدن در فروشگاه) توسط
(5) f(موجودی) = 1-Exp(-موجودی/آستانه)
داده میشود. با این حال، آستانه تجمیع ممکن است با آستانه فروشگاه فردی متفاوت باشد (و هیچ دلیل قانعکنندهای برای مطابقت f() تجمیع با f() فردی وجود ندارد؛ این فقط یک روش ساده برای شروع بود).
در مجموعه Store[]، من مجموعهای از فروشگاههای فردی را محاسبه میکنم، که کاملاً پیوسته به نظر میرسند، حتی اگر جمعیت فقط 100 باشد. (بیش از 100000 پمپ بنزین در ایالات متحده وجود دارد.)
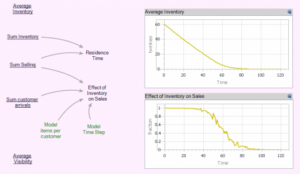
توجه داشته باشید که رفتار سری زمانی اثر موجودی بر فروش سیگموئیدی است.
اکنون میتوانیم رفتار فردی و تجمیعی را مقایسه کنیم:
موجودی
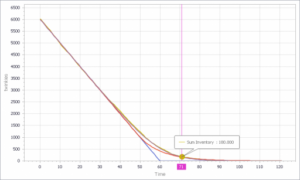
فروش
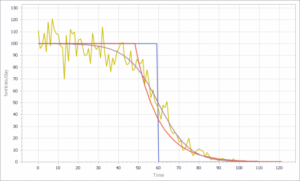
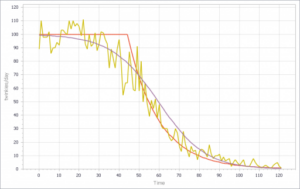
خط زرد پر سر و صدا مجموع فروشگاههای فردی است. خط آبی از اعمال یک برش سخت، معادله (1) بالا، ناشی میشود. این مانند این است که فرض کنیم همه فروشگاهها برابر هستند، و موجودی تا زمانی که تمام نشده است، بر فروش تأثیر نمیگذارد. واضح است که تناسب خوبی نیست، اگرچه ممکن است یک میانبر کافی باشد که در آن پویایی موجودی واقعاً تمرکز یک مدل نیست.
خط قرمز همچنین یک محدودیت موجودی/tau را اعمال میکند، اما ثابت زمانی (tau ) بسیار طولانیتر از گام زمانی، در 8 روز (گام زمانی = 1 روز) است. در نهایت، خط سیگموئیدی بنفش از اعمال محدودیت غیرخطی f(موجودی) ناشی میشود. این تناسب بسیار خوبی است، اما آستانه برای تجمیع باید حدود دو برابر بزرگتر از فروشگاههای فردی باشد.
با این حال، اگر f() را به طور ضعیف پارامتربندی کنید، و محدودیت موجودی/تاو را حذف کنید، آنچه به نظر میرسد نوسانات آشفته است – جالب، اما آشکارا غیرفیزیکی – به دست میآورید:
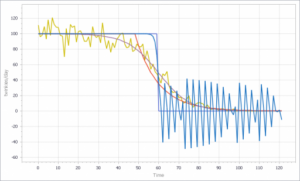
اگر علاوه بر این، تنوع در نرخ ورود مشتری فروشگاه را اضافه کنید، دم طولانیتری در موجودی به دست میآورید. آن آخرین توینکی احتمالاً در یک فروشگاه کم تردد خواهد بود. این کار را کمی سختتر میکند تا تمام قسمتهای منحنی را برازش دهید:
فکر میکنم سوالات جالبی در اینجا وجود دارد که میتواند یک مقاله عالی برای کنفرانس SD باشد:
- (تحت چه شرایطی) میتوانید شکل تابعی محدودیت تجمیع را از ویژگیهای فروشگاههای فردی استخراج کنید؟
- چه زمانی کاستیهای رویکردهای میانبر، که ممکن است مشتقات صاف نداشته باشند، در مدلهای تجمیعی مانند پویایی صنعتی مهم هستند؟
- پیامدهای عملی برای مدلهای بازاریابی چیست؟
- از دادههای تجمیعی به تنهایی چه چیزی میتوان در مورد سطوح موجودی استنباط کرد؟
- آیا واقعاً آشفتگی است؟
شروع کنید!
مدل ونسیم آن را تهیه کنید.