فجایع جفت شده
من به این مقاله جالب در مورد پویایی شبکه برخورد کردم و فکر کردم این مدل یک کاربرد جالب برای Ventity خواهد بود:
چارلز دی. برومیت، جورج بارنت و رایسا ام. دسوزا
چکیده
یک چالش مهم در چندین رشته، درک چگونگی انتشار تغییرات ناگهانی در میان سیستمهای جفت شده است. نمونهها شامل همگامسازی چرخههای تجاری، فروپاشی جمعیت در اکوسیستمهای تکهای، تغییر بازار به یک پلتفرم فناوری جدید، فروپاشی قیمتها و اعتماد در بازارهای مالی و فوران اعتراضات در چندین کشور است. تعدادی از مدلهای ریاضی این پدیدهها دارای تعادلهای متعدد هستند که توسط دوشاخههای زین-گره از هم جدا شدهاند. ما این رفتار را در شکل نرمال خود به عنوان معادلات دیفرانسیل معمولی سریع-آهسته مطالعه میکنیم. در مدل ما، یک سیستم از زیرسیستمهای متعدد مانند کشورها در اقتصاد جهانی یا تکههای یک اکوسیستم تشکیل شده است. هر زیرسیستم توسط یک کمیت اسکالر مانند خروجی اقتصادی یا جمعیت توصیف میشود که از طریق دوشاخههای زین-گره دچار تغییرات ناگهانی میشود. زیرسیستمها از طریق کمیت اسکالر خود جفت میشوند (به عنوان مثال، تجارت خروجی اقتصادی را جفت میکند؛ انتشار جمعیتها را جفت میکند)؛ آن جفتسازی مکانهای دوشاخههای آنها را جابجا میکند. این مدل دو روش را نشان میدهد که تغییرات ناگهانی میتوانند در آنها منتشر شوند: آنها میتوانند آبشاری شوند (یکی باعث دیگری شود) یا میتوانند از روی زیرسیستمها جهش کنند. مورد دوم در مدلهای کلاسیک آبشارها وجود ندارد. برای یک کاربرد، ما اعتراضات بهار عربی را مطالعه میکنیم. پس از اتصال مدل به نظریههای جامعهشناختی که دارای دوپایداری هستند، از دادههای اجتماعی-اقتصادی برای تخمین نزدیکیهای نسبی به نقاط اوج و از دادههای فیسبوک برای تخمین جفتسازیها در میان کشورها استفاده میکنیم. ما دریافتیم که اگرچه اعتراضات تمایل به گسترش محلی دارند، اما به نظر میرسد مانند مدل سبکسازی شده، از روی کشورها نیز “جهش” میکنند؛ این نتیجه یک کلاس جدید از موتیفهای زمانی را در مجموعههای دادههای شبکه طولی برجسته میکند.
Ventity در اینجا منطقی است زیرا سیستم از شبکهای از حالتهای جفت شده تشکیل شده است. Ventity نمایش طیف گستردهای از معماریهای شبکه را آسان میکند. این بدان معناست که دو نوع موجودیت در سیستم وجود دارد: “گرهها” و “جفتسازیها”.
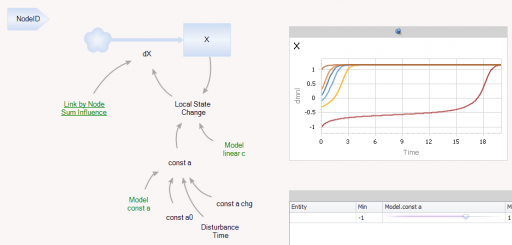
نوع موجودیت گره شامل یک حالت واحد (X) با بازخورد محلی و همچنین تأثیر از راه دور از جفتسازی و چند پارامتر جهانی است که از موجودیت مدل ارجاع داده میشوند:
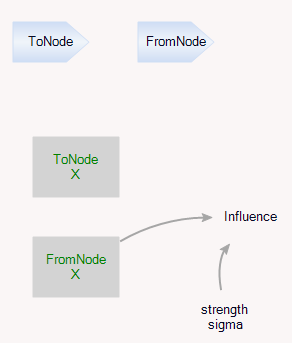
جفتسازی به سادگی یک ارجاع از یک گره به گره دیگر با یک پارامتر قدرت است:
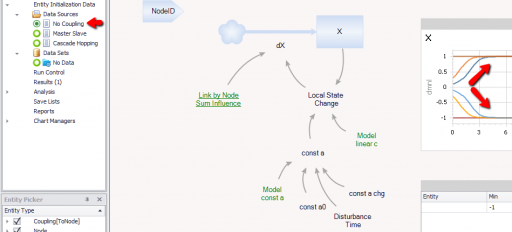
اگر هیچ جفتسازی ایجاد نکنید، گرهها به صورت مستقل اجرا میشوند، همانطور که در بخش 2.1 مقاله آمده است. میتوانید از آن برای دیدن چگونگی ایجاد یک نقطه اوج توسط پویایی دوپایدار X با اجرای مجموعهای از گرهها با شرایط اولیه مختلف استفاده کنید:
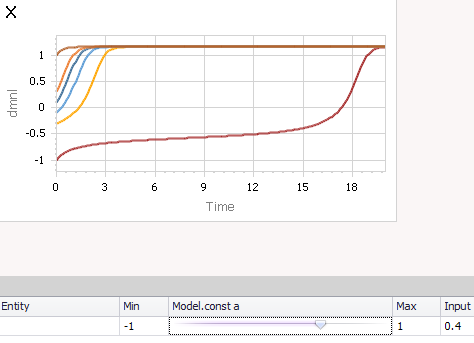
با افزایش Model.const a جهانی، میتوانید یک دوشاخه را القا کنید که شاخه پایین سیستم را ناپایدار میکند، به طوری که همه مسیرها تمایل به افزایش دارند:
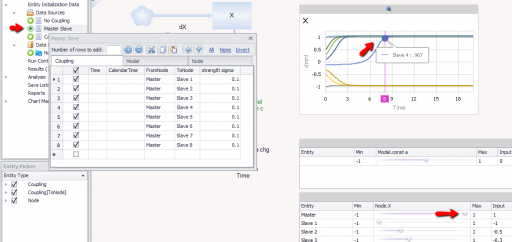
بخش 2.2 مقاله یک سیستم ارباب-برده را با دو گره و یک جفتسازی واحد نشان میدهد که توسط آن گره ارباب بر برده تأثیر میگذارد. من در واقع این را با یک ارباب واحد که چندین برده را هدایت میکند، تنظیم کردم، جایی که هر برده X اولیه متفاوتی دارد. سپس افزایش X اولیه ارباب به جابجایی پایداری حالت اولیه برده 4 سرایت میکند:
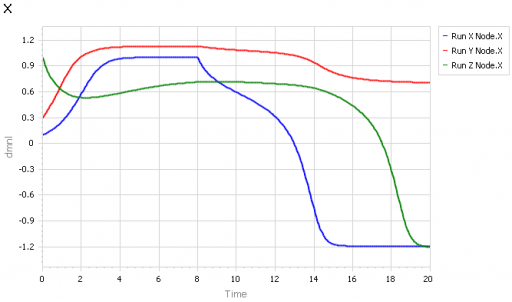
در بخش 2.3، با جهش آبشاری، اوضاع واقعاً جالب میشود. در این سناریو، سه گره جفت شده X -> Y -> Z وجود دارد. X (آبی) در زمان 8 با تغییر پارامتر const a محلی خود، به صورت برونزا مختل میشود و باعث میشود از یک مقدار پایدار نزدیک به 1 به حدود 1.2- منتقل شود. این به نوبه خود باعث یک تغییر جزئی در حالت Y (قرمز) میشود، اما به دلیل جفتسازی ضعیف، برای ناپایدار کردن Y کافی نیست. با این حال، تغییر کوچک در Y برای هل دادن Z از حالت خود کافی است و باعث انتقال ناگهانی به 1.2- در حدود زمان 18 میشود.
در نظر بگیرید که این چه تأثیری بر هر تفکر ساده مبتنی بر همبستگی یا یک مدل رگرسیون خواهد داشت. X به وضوح باعث یک تغییر فاجعهبار در Z شده است، اما بدون تغییر آشکار در Y. در حضور نویز، به راحتی میتوان نتیجه گرفت که همه اینها یک تصادف بوده است. (اگر در مورد علیت شک دارید، فقط const a chg گره X را روی صفر تنظیم کنید و ببینید چه اتفاقی میافتد.)
من شما را تشویق میکنم که به مقاله اصلی نگاهی بیندازید – نمودارهای فاز خوبی دارد و به بررسی برخی از کاربردهای جالب میپردازد. فکر میکنم از همان ساختار میتوان برای پیادهسازی یک مقاله پویایی شبکه جالب دیگر استفاده کرد: تعاملات مؤثر وابسته به حالت در شبکههای نوسانگر از طریق توابع جفتسازی با مناطق مرده. و اگر این موضوع را دوست دارید، فاجعه شبکه: الگوهای خودسازمان یافته هم ناپایداری و هم ساختار شبکههای پیچیده را آشکار میکنند، کاربردهای داده محور جالبتری دارد.
یک گسترش جالب از این مدل، تعمیم به شبکههای بزرگتر با اصلاح دادههای ورودی یا استفاده از اقدامات برای تولید شبکههای تصادفی خواهد بود.