گیدو ولف رایشرت سوال جالبی را در math.stackexchange مطرح میکند:
این سوال به مقاله مفیدی از مکس کلمان، کاوه دیانتی و ماتئو پدرچینی در مجموعه مقالات ISDC 2022 اشاره میکند.
من از ارجاعی که مستقیماً به این سوال مرتبط باشد اطلاعی ندارم، اما گمان میکنم که کندوکاو در ریشههای اقتصادی این جایگزینها نشان دهد که کشسانی (Elasticities) معمولاً در موقعیتهای غیرپویا، با علت و معلول نزدیک، مانند منحنی تقاضای معمولی Q=P^e، استفاده میشد (و میشود)، که در آن نسخه اول راحتتر است. در هر صورت، مفهوم اقتصادی کشسانی در سال 1890، مدتها قبل از اقتصادسنجی، که اساساً فرزند عصر محاسبات است، معرفی شد. از نظر عملی، در بسیاری از موقعیتها، دو تفسیر از نظر عملکرد معادل خواهند بود، اما تفاوتهای مهمی در موارد حاشیهای وجود دارد.
اگر رابطه بین x و y جعبه سیاه باشد، یعنی شما شکل تابعی را نداشته باشید یا نتوانید آن را حل کنید، روش مشتق زمانی (نسخه دوم) ممکن است تنها رویکرد ممکن باشد. این نادر به نظر میرسد. (این موضوع گهگاه در برخی از زبانهای اولیه SD که فاقد تابعی برای استخراج شیب از جدول جستجو بودند، مطرح میشد.)
با این حال، نسخه مشتق زمانی با چند چالش روبرو است. در یک شبیهسازی واقعی، dt یک تفاوت محدود است، بنابراین شما یک مشکل مقداردهی اولیه خواهید داشت: در شروع شبیهسازی، dx/dt و dy/dt مشاهده شده صفر خواهند بود و اپسیلون تعریف نشده خواهد بود. همچنین ممکن است مشکلاتی در مورد تأخیرهای کوچک ناشی از dt محدود و حساسیت به نویز داشته باشید.
فرمولبندی رایج کشسانی ثابت،
Y = Yr*(X/Xr)^elasticity
خودش در بسیاری از موارد مشکلساز است، زیرا برای از بین بردن تقاضا به قیمت بینهایت نیاز دارد و در قیمت 0 تقاضای بینهایت ایجاد میکند. یک مشکل ظریفتر این است که شیب این رابطه،
Y = elasticity*Yr/Xr*(X/Xr)^(elasticity-1)
برای 0 < کشسانی < 1، شیب این رابطه با نزدیک شدن X به 0 از سمت مثبت به بینهایت نزدیک میشود. این موضوع حلقههای بازخورد با بهره بینهایت در اطراف آن نقطه ایجاد میکند و میتواند منجر به رفتار شدید شود.
کشسانی ثابت با شیب شدید نزدیک به 0، e=.5
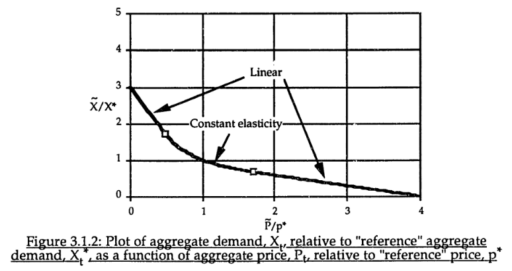
برای استحکام، ممکن است به یک شکل تابعی جایگزین نیاز باشد. به عنوان مثال، در آزمایشهای بازار، کامپمان قطعات خطی را به منحنی تقاضای کشسانی ثابت مرکزی متصل کرد: https://dspace.mit.edu/handle/1721.1/13159?show=full (صفحه 147):
گزینه دیگر تغییر شکلهای تابعی است. منطقی است که فرض کشسانی ثابت را کنار بگذاریم. یک روش خوب برای انجام این کار برای یک منحنی عرضه با شیب رو به بالا یا مشابه آن، استفاده از تابع تولید CES (کشسانی ثابت جایگزینی) است، که به طرز عجیبی وقتی با یک عامل ثابت استفاده میشود، کشسانی ثابت ندارد. معادله به این صورت است:
Y = Yr*(b + (1-b)*(X/Xr)^p)^(1/p)
با
p = (s-1)/s
که s کشسانی جایگزینی است. تفسیر تابع تولید b این است که سهم یک عامل ثابت در تولید خروجی Y را نشان میدهد. به طور کلی، s و b شکل منحنی را کنترل میکنند، که به طور مناسب از (0،0) و (Xr،Yr) عبور میکند. دو تفاوت کلیدی بین این شکل و فرمولبندی کشسانی مانند Y=X^e وجود دارد:
- شیب در 0،0 محدود باقی میماند.
- یک حد بالایی برای Y برای X بزرگ وجود دارد.
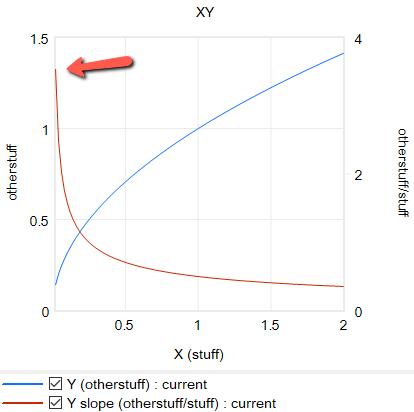
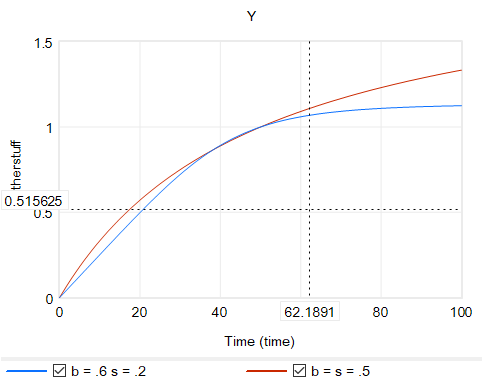
خروجی Y از CES با یک عامل ثابت برای دو مجموعه مقادیر b و s.
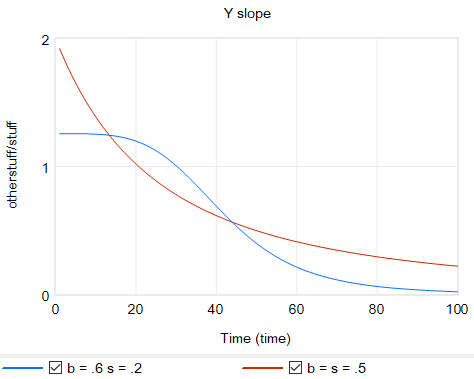
شیب برای همان نمونههای CES.
گزینه دیگری که اغلب مفید است، استفاده از تابع سیگموئید است.
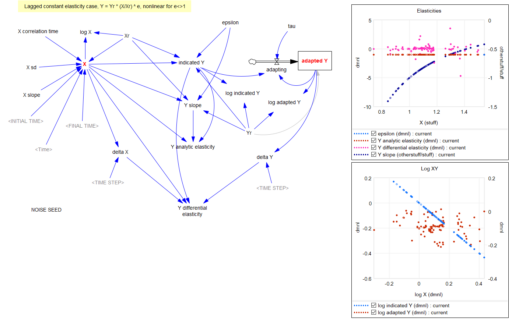
با بازگشت به سوال اصلی، در مورد مزایای (dy/y)/(dx/x) در مقابل شکل مشتق زمانی (dy/dt)/(dx/dt)x/y، فکر میکنم یک ملاحظه اضافی وجود دارد: اگر علیت دقیقاً نزدیک نباشد، بلکه شامل یک انتگرال باشد، چه؟ به عنوان مثال، ممکن است چیزی شبیه به این داشته باشیم:
Y* = Yr*(X/Xr)^elasticity ~ indicated Y Y = SMOOTH( Y*, tau ) ~ actual Y with an adaptation lag tau
البته این با استفاده از نمادگذاری quasi-Vensim است. در این حالت، اگر dY/dt را مشاهده کنیم و آن را با dX/dt مقایسه کنیم، ممکن است گمراه شویم، زیرا اثر کشسانی با اثر تأخیر tau مخلوط میشود. این امر به ویژه در صورتی صادق است که tau نسبت به افقی که در آن رفتار را مشاهده میکنیم، طولانی باشد.
کشسانی ثابت با نویز و انبار مداخلهگر.
این کلمات زیادی است که به طور بالقوه از سوال اصلی گیدو طفره میرود، اما امیدوارم مفید واقع شود.
برای کامل بودن، در اینجا چند نمونه از برخی از ویژگیهای مورد بحث در بالا آورده شده است. اینها باید در Vensim از جمله PLE رایگان اجرا شوند (لطفاً اگر مشکلی پیدا کردید نظر دهید).
- elasticity-constant 1: کشسانی ثابت، Y = Yr*(X/Xr)^e
- elasticity-lookup 1: کشسانی، با Y = Yr*LookupTable(X/Xr)
- elasticity-linear 1: کشسانی، با شیب خطی، Y = Yr + c*(X-Xr)
- elasticity-CES 1: کشسانی با تابع تولید CES و یک عامل ثابت، Y = Yr*(b + (1-b)*(X/Xr)^p)^(1/p)
- elasticity-stock-tau 1: کشسانی ثابت با یک انبار مداخلهگر